Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AB//CD, áp dụng định lý Ta-lét, ta có: O A O C = O B O D
Từ đó suy ra ĐPCM
Cho hình thang ABCD có hai đáy là AB và CD, các đường chéo cắt nhau tại O. Chứng minh: OA.OD = OB.OC

Xét tam giác OAB và tam giác OCD ta có :
^AOB = ^COD ( đối đỉnh )
^OAB = ^OCD ( so le trong )
Vậy tam giác OAB ~ tam giác OCD ( g.g )
=> OA/OC = OB/OD => OA.OD = OC.OB
Vì AB//CD nên:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\) ( hệ quả đl ta-lét)
từ đó suy ra : OA.OD=OB.OC(đpcm)

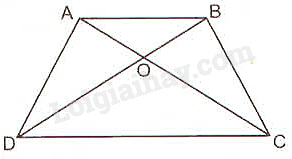
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).


Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).


Dễ chứng minh \(\Delta ABD=\Delta BAC\) (c.g.c)
\(\Rightarrow\widehat{DBA}=\widehat{CAB}\Rightarrow\Delta OAB\text{ cân tại O}\Rightarrow OA=OB\) (1)
Mặt khác cũng do \(\Delta ABD=\Delta BAC\) suy ra BD = AC hay OB + OD = OA + OC
Do (1) suy ra OD = OC (2)
Nhân theo từng vế hai đẳng thức (1) và (2) ta được đpcm: OA . OD = OB . OC
P/s: Thực ra ban đầu em chẳng có ý tưởng thế này đâu. Nhưng vừa làm xong bài Câu hỏi của Nguyễn Thị Phương Uyên nên mới nghĩ ra hướng chứng minh tương tự thế này đấy ạ:)

Ta có: AB // CD (gt), áp dụng hệ quả của định lý Ta – lét ta có:
Suy ra ![]() (hệ quả định lí ta-lét)
(hệ quả định lí ta-lét)
Vậy OA.OD = OB.OC

a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: ˆACD=ˆBDCACD^=BDC^
hay ˆODC=ˆOCDODC^=OCD^
Xét ΔOCD có ˆODC=ˆOCDODC^=OCD^
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
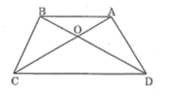
Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{DOC}\)
Do đó: ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)