Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta nhận xét :
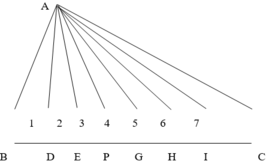
- khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD và ADC. Số tam giác đếm được là 3 : ABC, ADB và ADC. Ta có : 1 + 2 = 3 (tam giác)
- khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số tam giác đếm được là 6 :
ABC, ABD, ADE, ABE, ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)
Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)
Cách 2 :- Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)
Lập luận tương tự như trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.
Vậy số tam giác tạo thành là : 7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).

a nhận xét:
- Khi lấy 1 điểm tạo thành 2 hình tam giác đơn và có 3 hình tam giác trên hình vẽ là : ABD ; ADC và ABC. Ta có :
1 + 2 = 3 (hình)
- Khi lấy 2 điểm thì tạo thành 3 hình tam giác đơn và có 6 hình tam giác trên hình vẽ là : ABD ; ADE ; AEC ; ABE ; ADC ; ABC.
Ta có : 1 + 2 + 3 = 6 (hình).
Vậy khi lấy 6 điểm ta sẽ có 7 hình tam giác đơn được tạo thành trên hình vẽ và số hình tam giác có trên hình vẽ là :
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28...

Đề bài thiếu dữ kiện nếu không cho vị trí cuat điểm E hoặc điểm M. Nhìn hình vẽ tôi tạm cho E là điểm giữa của AN
Theo đề bài suy ra \(\frac{AE}{AC}=\frac{1}{4}\) Xét tg ABE và tg ABC có chung đường cao từ B->AC nên
\(\frac{S_{ABE}}{S_{ABC}}=\frac{AE}{AC}=\frac{1}{4}\Rightarrow S_{ABE}=\frac{S_{ABC}}{4}\Rightarrow S_{BCE}=S_{ABC}-S_{ABE}=\frac{3xS_{ABC}}{4}\)
Twd đề bài suy ra \(\frac{EN}{EC}=\frac{1}{3}\) xét tg BEN bà tg BCE có chung đường cao từ B->AC nên
\(\frac{S_{BEN}}{S_{BCE}}=\frac{EN}{EC}=\frac{1}{3}\)
Xét tg BEN và tg BEM có chung đáy BE và đường cao từ N->BE = đường cao từ M->BE nên \(S_{BEN}=S_{BEM}\)
Xét tg BEM và tg BCE có chung đường cao từ E->BC nên
\(\frac{S_{BEM}}{S_{BCE}}=\frac{BM}{BC}=\frac{S_{BEN}}{S_{BCE}}=\frac{1}{3}\Rightarrow S_{BEM}=\frac{S_{BCE}}{3}\)
\(\Rightarrow S_{EMC}=S_{BCE}-S_{BEM}=S_{BCE}-\frac{S_{BCE}}{3}=\frac{2xS_{BCE}}{3}=\frac{2x3xS_{ABC}}{3x4}=\frac{S_{ABC}}{2}\)
\(\Rightarrow S_{AEMB}=S_{ABC}-S_{EMC}=S_{ABC}-\frac{S_{ABC}}{2}=\frac{S_{ABC}}{2}\)
\(\Rightarrow S_{EMC}=S_{AEMB}\)


chữ đẹp quá