Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thể tích cần tìm là thể tích khối tròn xoay khi quay diện tích hình phẳng giới hạn bởi (P) đường thẳng x = 0, x= 2 khi quay quanh Ox trừ thể tích hình nón tạo thành khi quay tam giác tạo với tiếp tuyến, đường thẳng x = 2 quanh Ox


vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra
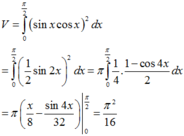

Đáp án D