Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
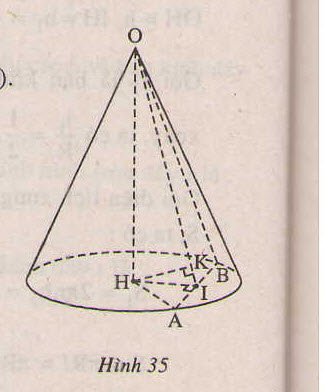
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
Đáp án D.
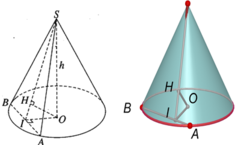
Giả sử hình nón có đỉnh S, đáy là đường tròn tâm I bán kính r, thiết diện đi qua đỉnh là ∆ S A D cân tại S.
Gọi J là trung điểm của AB, ta có A B ⊥ I J A B ⊥ S I → A B ⊥ S I J → S A B ⊥ S I J
Trong mặt phẳng (SIJ): Kẻ I H ⊥ S J , H ∈ S J
Từ S A B ⊥ ( S I J ) ( S A B ) ∩ ( S I J ) = S J → I H ⊥ S A B → I H = d ( I ; ( S A B ) ) = 24 ( c m ) I H ⊥ S J
1 I H 2 = 1 S I 2 + 1 S J 2 → 1 I J 2 = 1 24 2 - 1 40 2 = 1 900 → I J = 30
→ S J = S I 2 + I J 2 = 50 ( c m )
A B = 2 J A = 2 r 2 - I J 2 = 2 50 2 - 30 2 = 80 ( c m )
Vậy S ∆ S A B = 1 2 S J . A B = 1 2 . 50 . 80 = 2000 ( c m 2 )
Đáp án D
Ta có: 1 d 2 I ; α = 1 d 2 + 1 h 2 trong đó d là khoảng cách từ tâm của đáy đến giao tuyến của α và đáy.
Khi đó d = 15 ⇒ độ dài dây cung a = 2 r 2 − d 2 = 40 ; đường cao thiết diện = h 2 + d 2 = 25
Do đó A = 1 2 a . h ' = 1 2 .40.25 = 500 c m 2 .
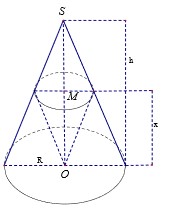
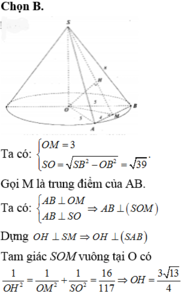
∆ O S A vuông cân OA = Ó = 1. ∆ S A B đều suy ra AB = 2 .
Kẻ O I ⊥ A B ⇒ O I = 1 2 A B = 2 2 .
Kẻ O H ⊥ S I ⇒ O H = d = 3 3
Đáp án B
Đáp án C
Gọi R = 10 và r lần lượt là bán kính đát của hình nón lớn và hình nón nhỏ.
Ta có:
r R = S M S O = S O − M O S O ⇔ r 10 = 3 5 ⇔ r = 6 c m
Diện tích xung quanh của hình nón nhỏ là S x q = π r S M 2 + r 2 = 36 π 26 c m 2
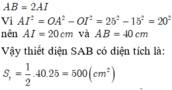
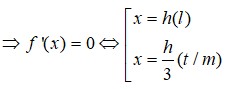
Đáp án A.