Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.

Chọn đáp án C.
Gọi h và l lần lượt là độ dài chiều cao và độ dài đường sinh của hình nón đã cho. Theo giả thiết thì l = 3r
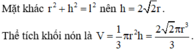

Đáp án D
Thể tích khối nón là V = 1 3 π r 2 h = 1 3 π 3 2 .4 = 4 π

Chọn B.
Phương pháp:
Sử dụng công thức tính thể tích khối nón có bán kính đáy r và chiều cao h là
V = 1 3 πτ 2 h
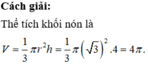

Đáp án D
Thể tích khối nón là V = 1 3 π r 2 h = 1 3 π 3 2 .4 = 4 π

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đáp án A
Ta có:
l = 2 r ⇒ h = l 2 − r 2 = r 3 ⇒ V = 1 3 π r 2 h = π r 3 3 3