Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)

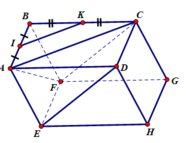
I và K lần lượt là trung điểm của các cạnh AB và BC ⇒ IK là đường trung bình của ∆ABC nên IK // AC ⊂ (AFC) ⇒ IK // (AFC)
hình hộp ABCD.EFGH nên các mặt của hình hộp là hình bình hành.
Suy ra: EF// CD(cùng // GH) và EF = CD ( cùng = GH)
EFCD là hình bình hành
⇒ ED // CF
Nên ED // (AFC)
⇒ ba vecto A F → , I K → , E D → đồng phẳng (vì giá của chúng song song với một mặt phẳng)
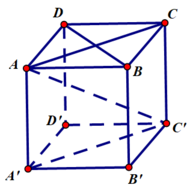

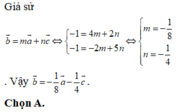
\(\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{AB}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AF}-\overrightarrow{AC}+\overrightarrow{AH}=\overrightarrow{AE}+\overrightarrow{AB}-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AF}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AH}\)