Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42

A B C D A' B' C' D' I J
a) Có AA' // DD' và AB//DC nên \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\).
b) Do \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\) và \(\left(\beta\right)\cap\left(AA'B'B\right)=A'B'\) và \(\left(\beta\right)\cap\left(CC'D'D\right)=C'D'\) nên \(A'B'\) // \(C'D'\).
Chứng minh tương tự B'C'//D'A'.
Do đó tứ giác A'B'C'D' là hình bình hành và J là trung điểm của A'C'.
Suy ra: IJ là đường trung bình của hình thang A'C'CA nên IJ // AA'.
c) Tương tự IJ là đường trung bình của hình thang B'D'DB \(IJ=\dfrac{\left(B'B+DD'\right)}{2}\).
Theo câu b IJ là đường trung bình của hình thang A'C'CA nên \(IJ=\dfrac{\left(AA'+CC'\right)}{2}\).
Suy ra: \(BB'+DD'=AA'+CC'\) hay \(DD'=a+c-b\).
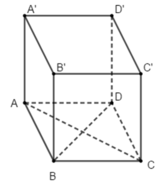







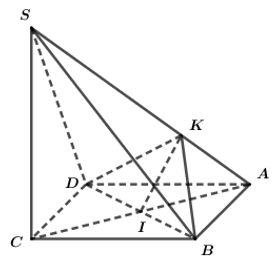



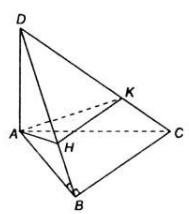

Ta có: B D ⊥ A C B D ⊥ A A ' ⇒ B D ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( A B C D ) ⇒ ( A B C D ) ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( B D C ' ) ⇒ ( B D C ' ) ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( A ' B D ) ⇒ ( A ' B D ) ⊥ ( A C C ' A ' )
Vậy mp(CDD’C’) không vuông góc với mặt phẳng (ACC’A’).
Chọn B.