Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Từ $a+b+c=2; \frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}=2,5$
$\Rightarrow (a+b+c)\left(\frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}\right)=5$
\(\Leftrightarrow \frac{a}{a+b}+\frac{a}{a+c}+\frac{a}{b+c}+\frac{b}{a+b}+\frac{b}{a+c}+\frac{b}{b+c}+\frac{c}{a+b}+\frac{c}{a+c}+\frac{c}{b+c}=5\)
\(\Leftrightarrow \frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}+\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=5\)
\(\Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=2\)
Khi đó:
\(A=\frac{a-(b+c)}{b+c}+\frac{b-(c+a)}{c+a}+\frac{c-(a+b)}{a+b}=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}-3\)
\(=2-3=-1\)
Vậy $A=-1$

\(A=\left\{a_1,a_2,...,a_k,c_1,c_2,...,c_j\right\}\\ B=\left\{b_1,b_2,...,b_m,c_1,c_2,...,c_j\right\}\\ \left|A\right|=k+j,\left|B\right|=m+j\\ A\cup B=\left\{a_1,a_2,...,a_k,b_1,b_2,...,b_m,c_1,c_2,...,c_j\right\}\Rightarrow\left|A\cup B\right|=m+k+j\\ A\cap B=\left\{c_1,c_2,...,c_j\right\}\Rightarrow\left|A\cap B\right|=j\)
\(\left|A\cup B\right|=k+j+m+j-j=\left|A\right|+\left|B\right|-\left|A\cap B\right|\)

Một cách dựa vào hàm số:
Đặt \(VT=f\left(x\right)\)
- Nếu 2 trong 3 số a, b, c bằng nhau hoặc một trong 3 số bằng 0 thì pt hiển nhiên có nghiệm
- Nếu không có bất cứ cặp nào bằng nhau và đều khác 0, do tính đối xứng của \(f\left(x\right)\) , không làm mất tính tổng quát, giả sử \(a>b>c\) ta có:
\(f\left(a\right)=a\left(a-b\right)\left(a-c\right)\)
Do \(\left(a-b\right)\left(a-c\right)>0\Rightarrow f\left(a\right)\) cùng dấu với \(a\) \(\Rightarrow a.f\left(a\right)>0\) (1)
\(f\left(b\right)=b\left(b-c\right)\left(b-a\right)\)
Do \(\left(b-c\right)\left(b-a\right)< 0\Rightarrow b.f\left(b\right)< 0\) (2)
\(f\left(c\right)=c\left(c-a\right)\left(c-b\right)\)
Do \(\left(c-a\right)\left(c-b\right)< 0\Rightarrow c.f\left(c\right)>0\) (3)
- Nếu a, c cùng dấu \(\Rightarrow a;b;c\) cùng dấu \(\Rightarrow ab>0\)
Nhân vế với vế của (1) và (2): \(a.b.f\left(a\right).f\left(b\right)< 0\) \(\Rightarrow f\left(a\right).f\left(b\right)< 0\)
\(\Rightarrow\) Pt có ít nhất 1 nghiệm thuộc \(\left(a;b\right)\)
- Nếu \(a,\) c trái dấu \(\Rightarrow ac< 0\) nhân vế với vế của (1) và (3):
\(ac.f\left(a\right).f\left(c\right)>0\Rightarrow f\left(a\right).f\left(c\right)< 0\)
\(\Rightarrow\) Pt có ít nhất 1 nghiệm thuộc \(\left(a;c\right)\)
Vậy pt đã cho luôn luôn có nghiệm

11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)

heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp

\(\frac{P_nC_n^k}{n!A_n^k}=\frac{n!.\frac{n!}{k!\left(n-k\right)!}}{n!.\frac{n!}{\left(n-k\right)!}}=\frac{1}{k!}\)
Chắc là bạn ghi nhầm đề
Đáp án C.
- Phương pháp: Sử dụng công thức ba điểm và các vectơ bằng nhau.
- Cách giải:
+ Ta có: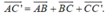
+ Mà: