Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

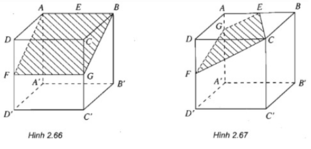
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

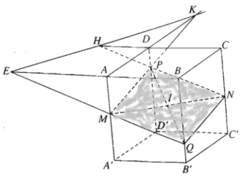
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.


Nối MN cắt CB kéo dài tại E
Nối EP kéo dài cắt B'C' tại F
Nối NP cắt A'B' kéo dài tại G
Nối GF kéo dài cắt C'D' tại H và A'D' kéo dài tại K
Nối MK cắt DD' tại Q
Thiết diện là lục giác MNPFHQ (lục giác này 6 cạnh dài bằng nhau và bằng 1 nửa đường chéo các mặt bên)

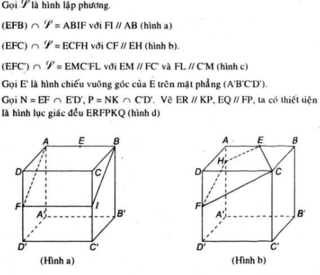
Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
- Mặt phẳng (EFB): ta vẽ FG //AB và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC'.
- (h.2.67) Mặt phẳng (EFC): Nối FC và vẽ EG // FC, ta được thiết diện là hình thang ECFG
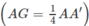
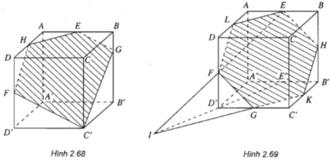
- (h.2.68) Mặt phẳng (EFC'): Nối FC' và vẽ EG // FC′. Nối GC' và vẽ FH // GC′. Ta được thiết diện là hình ngũ giác EGC'FH.
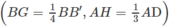
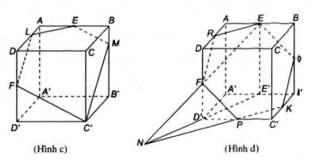
- (h.2.69) Mặt phẳng (EFK) với K là trung điểm của đoạn B'C'. Lấy trung điểm E' của đoạn A'B'. Ta có I = EF ∩ E′D. Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A'B'C'D'). Gọi G = IK ∩ C′D′. Nối F với G, vẽ EH // FG. Nối K với H, vẽ FL // KH và nối L với E. Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D'C', B'B, AD).