Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để A là số nguyên thì \(x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)
b: Để B là số nguyên thì \(2x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{1;0\right\}\)(do x là số nguyên)
c: Để C là số nguyên thì \(3x-3+10⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
hay \(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
d: Để D là số nguyên thì \(4x-1⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{4;2;14;-8\right\}\)

a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

a) Phương trình đường thẳng d có dạng: , với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
(1 ; 1 ; -1) vì
là vectơ pháp tuyến của (α).
Do vậy phương trình tham số của d có dạng:
c) Vectơ (2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên
cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương
(4 ; 2 ; -1) nên phương trình tham số có dạng:

Hướng giải quyết (làm biếng tính toán kiểu này :D):
- Nhận thấy ngay rằng B, C, D thẳng hàng nên A, B, C, D đồng phẳng
\(\Rightarrow\) khoảng cách từ O đến (ABC) và khoảng cách từ O đến (ACD) bằng nhau
\(\Rightarrow\) diện tích tam giác ABC = diện tích tam giác ACD
Mà hai tam giác này chung cạnh đáy AC
\(\Rightarrow\) khoảng cách từ B đến AC bằng khoảng cách từ D đến AC
\(\Rightarrow\) C là trung điểm của BD
Đến đây thì chắc là đơn giản lắm rồi
Okay, mình tính ra rồi, cảm ơn bạn. Có gì gợi ý giúp mình câu này luôn nhé.


4.
Qua G kẻ đường thẳng song song AB lần lượt cắt AC và BC tại M và N
\(\Rightarrow A'B'NM\) là thiết diện của (A'B'G) và lăng trụ
Theo Talet ta có \(\frac{CM}{AC}=\frac{CN}{BC}=\frac{2}{3}\Rightarrow CM=CN=\frac{2a}{3}\)
Kéo dài A'M, B'N, C'C đồng quy tại P (theo tính chất giao tuyến 3 mặt phẳng)
Do \(CN//B'C'\Rightarrow\frac{PC}{PC'}=\frac{CN}{B'C'}=\frac{2}{3}\Rightarrow\frac{PC}{PC+CC'}=\frac{2}{3}\)
\(\Rightarrow3PC=2\left(PC+a\right)\Rightarrow PC=2a\)
\(\Rightarrow PC'=3a\)
\(MN=\frac{2}{3}BC\Rightarrow S_{CMN}=\frac{4}{9}S_{ABC}=\frac{4}{9}.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{9}\)
\(V_{P.A'B'C'}=\frac{1}{3}PC'.S_{A'B'C'}=\frac{1}{3}.3a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{4}\)
\(V_{P.CMN}=\frac{1}{3}PC.S_{CMN}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{9}=\frac{2a^3\sqrt{3}}{27}\)
\(\Rightarrow V_{CMN.A'B'C'}=\frac{a^3\sqrt{3}}{4}-\frac{2a^3\sqrt{3}}{27}=\frac{19a^3\sqrt{3}}{108}\)
\(\Rightarrow V_{MNABA'B'}=\frac{a^3\sqrt{3}}{4}-\frac{19a^3\sqrt{3}}{108}=\frac{2a^3\sqrt{3}}{27}\)
2.
Đề thiếu dữ kiện ko tính được, chỉ tính được trong trường hợp tam giác ABC là vuông cân.
3.
\(AC=BC=a\sqrt{2}\) ; \(AC=AB\sqrt{2}=2a\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{BA'M}\) là góc giữa A'B và (ACC'A')
\(\Rightarrow\widehat{BA'M}=30^0\)
\(BM=\frac{1}{2}AC=a\)
\(tan\widehat{BA'M}=\frac{BM}{A'M}\Rightarrow A'M=\frac{BM}{tan30^0}=a\sqrt{3}\)
\(A'A=\sqrt{A'M^2-AM^2}=a\sqrt{2}\)
\(V=\frac{1}{2}A'A.AB.BC=a^3\sqrt{2}\)
Ko đáp án nào đúng

Lời giải:
Vì \(\frac{a}{b}\) chưa tối giản nên tồn tại một số \(d\in\mathbb{N}>1\) sao cho \(a\vdots d,b\vdots d\)
Khi đó \(a-b\vdots d\)
a)
Thấy $a$ và $a-b$ đều chia hết cho $d$ nên \(\frac{a}{a-b}\) không phải phân số tối giản
b) Vì \(a\vdots d\) và \(b\vdots d\) nên \(2a,2b\vdots d\). Do đó \(a-2b\vdots d\)
Thấy $2a$ và $a-2b$ đều chia hết cho $d$ nên \(\frac{2a}{a-2b}\) không phải phân số tối giản.
Ta có đpcm.
P/s: Phiền bạn từng sau đăng bài nên chú ý đăng đúng box. Bài này nên đăng ở box toán 6 thôi nhé.
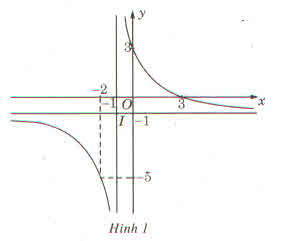

Chọn D