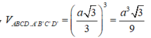Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()

Hướng dẫn: A
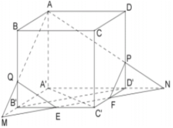
+ Đường cắt EF cắt A'D' tại N, M, AN cắt DD' tại P, AM cắt A'B' tại BB' tại Q. Từ đó mặt phẳng (AEF) cắt khối lăng trụ thành hai khối đó là ABCDC'QEFP và AQEFPB'A'D'.
+ Gọi
![]()
+ Do tính đối xứng của hình lập phương nên ta có V 4 = V 5
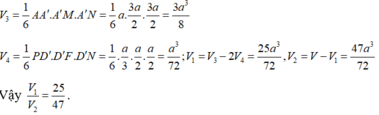

Nếu 3 cạnh a, b, c lập thành cấp số cộng thì ta có a + c = 2b
\(\Leftrightarrow\sin A+\sin C=2\sin B\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A-C}{2}=4\sin\frac{B}{2}\cos\frac{B}{2}\left(1\right)\)
Vì \(A+C=180^0-B\Rightarrow\frac{A+C}{2}=90^0-\frac{B}{2}\)
<=> \(\sin\frac{A+C}{2}=\sin\left(90^0-\frac{B}{2}\right)=\cos\frac{B}{2}\) hoặc \(\cos\frac{A+C}{2}=\cos\left(90^0-\frac{B}{2}\right)=\sin\frac{B}{2}\) (*)
Do đó (1) trở thành :
\(\Leftrightarrow\sin\frac{A+C}{2}\cos\frac{A-C}{2}=2\sin\frac{A+C}{2}\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\sin\frac{B}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}+\sin\frac{A}{2}\sin\frac{C}{2}=2\cos\frac{A}{2}\cos\frac{C}{2}-2\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}=3\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cot\frac{A}{2}\cot\frac{C}{2}=3\) => Điều phải chứng minh

Theo giả thiết ta có hệ : \(\begin{cases}A=90^0\\a,b,\frac{\sqrt{6}}{3},c\end{cases}\)\(\Leftrightarrow\begin{cases}a^2=b^2+c^2\\\frac{2}{3}b^2=ac\Leftrightarrow b^2=\frac{3}{2}ac\end{cases}\)
Từ đó suy ra \(a^2=\frac{3}{2}ac+c^2\Leftrightarrow2a^2=3ac+2c^2\Leftrightarrow\left(2a+c\right)\left(a-2c\right)=0\)
\(\Rightarrow a=2c\left(2a+c>0\right)\)
Mà \(\cos B=\frac{c}{a}=\frac{1}{2}\Rightarrow B=60^0,C=30^0\)
Vậy tam giác ABC là tam giác nửa đều

Đáp án B
Gọi O, O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. I là trung điểm đoạn OO'. Khi đó bán kính r của mặt cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' là:


\(\overrightarrow{n}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(1;-2;1\right)\) là một vectơ pháp tuyến của \(\left(\beta\right)\)
Mặt phẳng \(\beta\) đi qua A có vectơ pháp tuyến \(\overrightarrow{n}=\left(1;-2;1\right)\) có phương trình \(x-2y+z-2=0\)
Cho x, y là các số thỏa mãn \(x^2+y^2+xy=3\Leftrightarrow\left(x+y\right)^2-3=xy\)
Vì \(xy\le\frac{\left(x+y\right)^2}{4}\Leftrightarrow\left(x+y\right)^2-3\le\frac{\left(x+y\right)^2}{4}\)
\(\Leftrightarrow\left(x-y\right)^2\le4\)
Đáp án B
Đặt cạnh của hình lập phương là x
Từ đề bài ta có phương trình:
Vậy