Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
Bạn chỉ cần tìm sin, cos trong \(\left[0;2\pi\right]\) là đủ (vì cả 2 hàm đều tuần hoàn với chu kì \(2\pi\))
Đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\) với \(a\in\left[0;2\pi\right]\)
\(\Rightarrow4sina.cosa\left(2cos^2a-1\right)=1\)
\(\Leftrightarrow2sin2a.cos2a=1\Leftrightarrow sin4a=1\)
\(\Rightarrow4a=\frac{\pi}{2}+k2\pi\Rightarrow a=\frac{\pi}{8}+\frac{k\pi}{2}\)
\(\Rightarrow0\le\frac{\pi}{8}+\frac{k\pi}{2}\le2\pi\Rightarrow a=\left\{\frac{\pi}{8};\frac{5\pi}{8};\frac{9\pi}{8};\frac{13\pi}{8};\frac{17\pi}{8}\right\}\)
\(\Rightarrow\left(x;y\right)=\left(sin\frac{\pi}{8};cos\frac{\pi}{8}\right);\left(sin\frac{5\pi}{8};cos\frac{5\pi}{8}\right)...\)
2.
\(sinx=\frac{1}{3}\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+l2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)\\x=\pi-arcsin\left(\frac{1}{3}\right)\end{matrix}\right.\)
(Vì \(0< \frac{1}{3}< 1\) nên \(0< arcsin\left(\frac{1}{3}\right)< \frac{\pi}{2}\) do đó nếu \(k>0\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi>2\pi\) ; nếu \(k\le-1\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi\le-\frac{3\pi}{2}\) đều ko thuộc \(\left[0;\pi\right]\Rightarrow k=0\).
Tương tự với \(l\))
Cho mình hỏi sao từ 0 < 1/3 < 1 thì suy ra đc 0 < arcsin (1/3) < pi/2 vậy?

S A B C D H M N O
Cần câu d thôi đúng ko bạn?
\(ID\) cắt (SAC) tại A mà \(IA=2DA\Rightarrow d\left(I;\left(SAC\right)\right)=2d\left(D;\left(SAC\right)\right)\)
\(BD\) cắt (SAC) tại O mà \(OB=OD\Rightarrow d\left(D;\left(SAC\right)\right)=d\left(B;\left(SAC\right)\right)\)
Mặt khác \(BA=2HA\Rightarrow d\left(B;\left(SAC\right)\right)=2d\left(H;\left(SAC\right)\right)\)
\(\Rightarrow d\left(I;\left(SAC\right)\right)=4d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HM\perp AC\), từ H kẻ \(HN\perp SM\Rightarrow HN=d\left(H;\left(SAC\right)\right)\)
Áp dụng hệ thức lượng: (chú ý rằng \(AH=\frac{AB}{2}=\frac{a}{2};OH=\frac{AD}{2}=\frac{a\sqrt{2}}{2}\))
\(\frac{1}{HM^2}=\frac{1}{AH^2}+\frac{1}{OH^2}\Rightarrow HM=\frac{AH.OH}{\sqrt{AH^2+OH^2}}=\frac{a\sqrt{6}}{6}\)
\(\frac{1}{HN^2}=\frac{1}{SH^2}+\frac{1}{HM^2}\Rightarrow HN=\frac{SH.HM}{\sqrt{SH^2+HM^2}}=\frac{a\sqrt{57}}{19}\)
\(\Rightarrow d\left(I;\left(SAC\right)\right)=\frac{4a\sqrt{57}}{19}\)

Dễ dàng chứng minh \(SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SH \(\Rightarrow MN//HC\) (đường trung bình)
Trong mặt phẳng đáy, qua D kẻ đường thẳng song song HC cắt BA kéo dài tại P
\(\Rightarrow HC//\left(MNPD\right)\Rightarrow d\left(HC;DM\right)=d\left(HC;\left(MNPD\right)\right)=d\left(H;\left(MNPD\right)\right)\)
Trong mặt phẳng đáy, từ H kẻ \(HE\perp DP\)
\(\Rightarrow DP\perp\left(HEN\right)\)
Trong tam giác vuông HEN, từ H kẻ \(HF\perp EN\Rightarrow\left\{{}\begin{matrix}HF\perp EN\\HF\perp DP\end{matrix}\right.\)
\(\Rightarrow HF\perp\left(MNPD\right)\Rightarrow HF=d\left(H;\left(MNPD\right)\right)\)
\(SH=\frac{AB\sqrt{3}}{2}\Rightarrow SH=\frac{a\sqrt{3}}{2}\Rightarrow NH=\frac{a\sqrt{3}}{4}\)
\(AP=AH=\frac{a}{2}\Rightarrow DP=\sqrt{AP^2+AD^2}=\frac{3a}{2}\)
\(PH=CD=a\Rightarrow HE=PH.sin\widehat{DPA}=PH.\frac{AD}{DP}=\frac{2a\sqrt{2}}{3}\)
\(\frac{1}{HF^2}=\frac{1}{HE^2}+\frac{1}{NH^2}\Rightarrow HF=\frac{HE.NH}{\sqrt{HE^2+NH^2}}=a\sqrt{\frac{24}{155}}\)

11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)

16.
Đặt cạnh của đáy là x
\(DM=\sqrt{AD^2+AM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(\Rightarrow DM=CM\Rightarrow\Delta_vSMD=\Delta_vSMC\)
\(\Rightarrow SC=SD=2a\sqrt{5}\)
Mà \(SM\perp\left(ABCD\right)\Rightarrow\widehat{SCM}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCM}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}CM=SC.cos60^0=a\sqrt{5}\\SM=SC.sin60^0=a\sqrt{15}\end{matrix}\right.\) \(\Rightarrow AB=x=\frac{2CM}{\sqrt{5}}=2a\)
Gọi N là trung điểm CD \(\Rightarrow CD\perp\left(SMN\right)\)
\(AM//CD\Rightarrow AM//\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(M;\left(SCD\right)\right)\)
Từ M kẻ \(MM\perp SN\Rightarrow MH\perp\left(SCD\right)\Rightarrow MH=d\left(H;\left(SCD\right)\right)\)
\(MN=AB=2a\)
\(\frac{1}{MH^2}=\frac{1}{SM^2}+\frac{1}{MN^2}\Rightarrow MH=\frac{SM.MN}{\sqrt{SM^2+MN^2}}=\frac{2a\sqrt{15}}{\sqrt{19}}\)
14.
Do \(\widehat{C'BC}\) là góc giữa (ABCD) và (ABC') nên \(\widehat{C'BC}=60^0\)
\(\Rightarrow CC'=BC.tan60^0=a\sqrt{3}\)
15.
Gọi H là trung điểm BC \(\Rightarrow OH\perp BC\)
Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOH\right)\)
Từ O kẻ \(OK\perp SH\Rightarrow OK\perp\left(SBC\right)\Rightarrow OK=d\left(O;\left(SBC\right)\right)\)
\(OH=\frac{1}{2}AB=\frac{a}{2}\) ; \(AC=a\sqrt{2}\Rightarrow OA=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a\sqrt{2}}{2}\)
\(\frac{1}{OK^2}=\frac{1}{SO^2}+\frac{1}{OH^2}\Rightarrow OK=\frac{SO.OH}{\sqrt{SO^2+OH^2}}=\frac{a\sqrt{6}}{6}\)

a/ Do AB song song CD nên góc giữa SC và AB bằng góc giữa SC và CD
\(\Rightarrow\left(SC;AB\right)=\widehat{SCD}\)
Áp dụng định lý hàm cos:
\(cos\widehat{SCD}=\frac{SC^2+CD^2-SD^2}{2SC.CD}=\frac{4a^2+2a^2-4a^2}{2.2a.a\sqrt{2}}=\frac{\sqrt{2}}{4}\)
\(\Rightarrow\widehat{SCD}\approx69^0\)
b/ Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SCO}\) là góc giữa cạnh bên SC và mặt đáy (hay cũng là góc \(\widehat{SCA}\))
Ta có \(AC=AB\sqrt{2}=2a\) (đường chéo hình vuông)
\(\Rightarrow\Delta SAC\) đều
\(\Rightarrow\widehat{SCA}=60^0\)
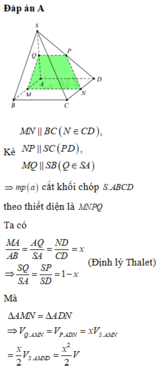
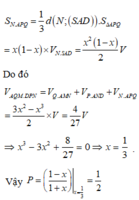
Đáp án B
Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng ( α ) chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.
Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau: