

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




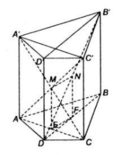
Hình bình hành ACC’A có hai đường chéo là
AC’ và A’C cắt nhau tại trung điểm Mcủa mỗi đường. Tương tự, hai đường chéo BD’ và B’D cắt nhau tại trung điểm N của mỗi đường.
b) Trung điểm E của AC là hình chiếu của trung điểm M của AC’ thep phương của cạnh lăng trụ. Tương tự, trung điểm F là hình chiếu trung điểm N của đường chéo BD’ trên BD. Ta có EM //CC′ và EM = CC′/2
Mặt khác FN // DD′ và FN = DD′/2. Từ đó suy ra tứ giác MNFE là hình bình hành và ta có MN = EF.

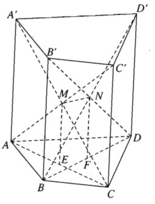
a) Gọi H là trung điểm của BC
△ABC có: E là trung điểm của AC, H là trung điểm của BC
Suy ra: EH // AB
Mà AB // A'B'
Do đó: EH // A'B' hay EH // B'F (1)
Ta có: EH // AB nên \(\dfrac{EH}{AB}=\dfrac{EC}{AC}=\dfrac{1}{2}\)
Mà AB = A'B', B'F = \(\dfrac{1}{2}\) A'B'
Nên: EH = B'F (2)
(1)(2) suy ra: EHB'F là hình bình hành. Do đó: EF // B'H
Mà B'H thuộc (BCC'B')
Suy ra: EF // (BCC'B')
b) Gọi K là trung điểm AB
Dễ dàng chứng minh được FKBB' là hình bình hành
Ta có: FK // BB'
Mà BB' // CC'
Suy ra: FK // CC' (1)
Ta có: FK = BB', mà BB' = CC'
Do đó: FK = CC' (2)
(1)(2) suy ra FKCC' là hình bình hành
Mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Nên C'K cắt CF tại trung điểm của hai đường thẳng
mà C'K thuộc (AC'B) , CF cắt (AC'B) tại I (đề bài)
Do đó: I là trung điểm của CF.

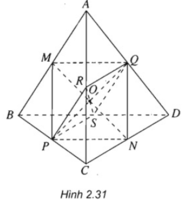
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

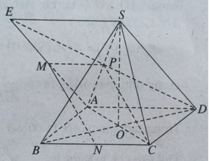
Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.