Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

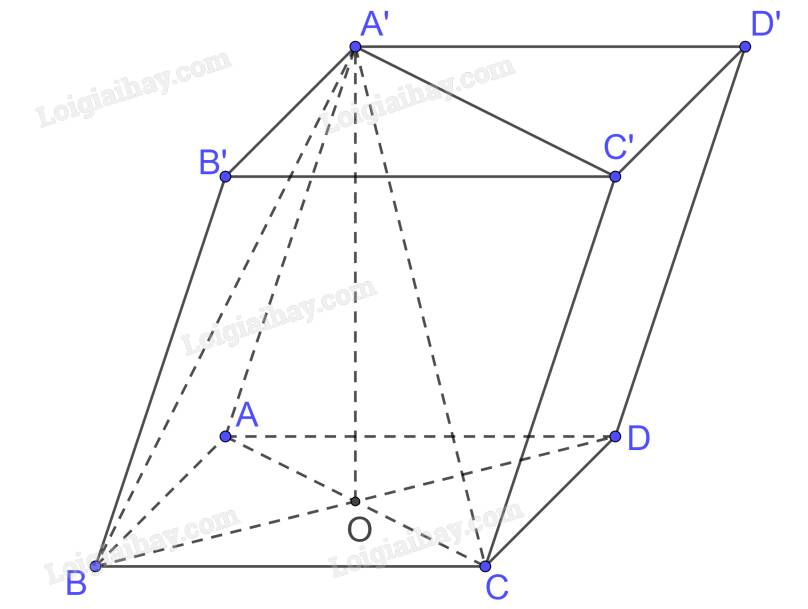
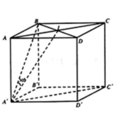
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)

a: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
b: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
c: Có 4 mặt bên là hình chữ nhật
d: Có tất cả là 6 mặt là hình chữ nhật

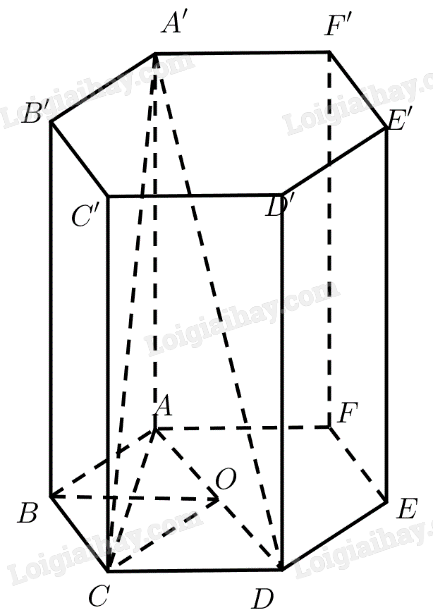
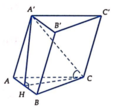
Tam giác \(ABC\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}} = a\sqrt 3 \)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)
\( \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).
Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).
\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)
\( \Rightarrow \Delta AA'D\) vuông tại \(A\)
\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}} = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).

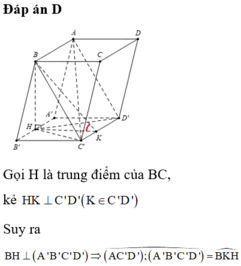


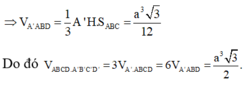






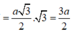
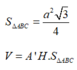
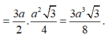
Đáp án B