Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

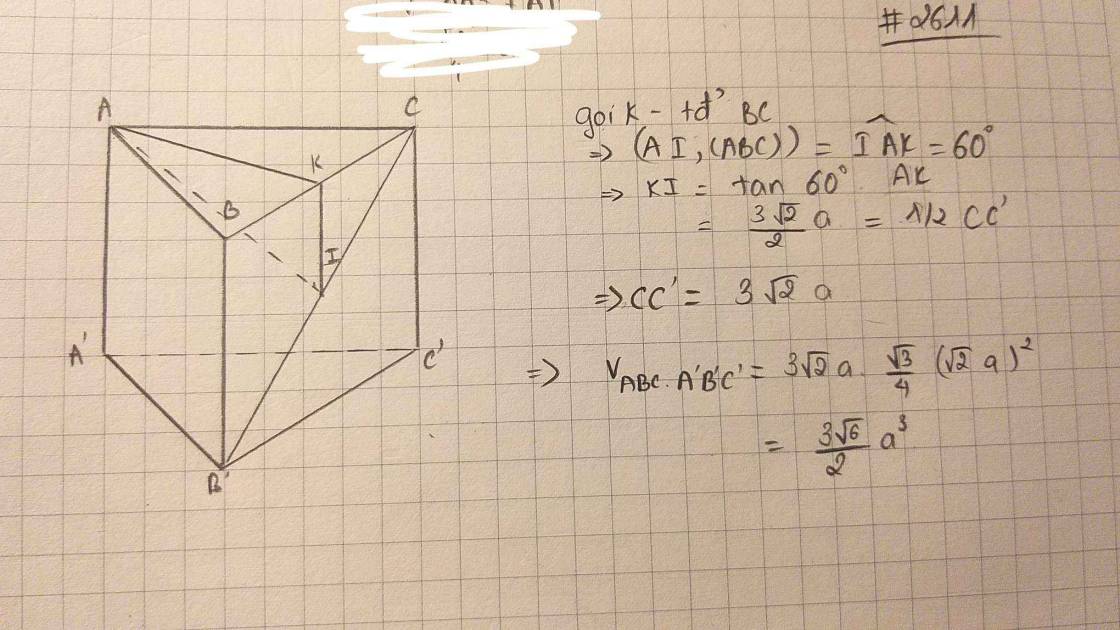
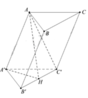
A H B C A' B' C' K I
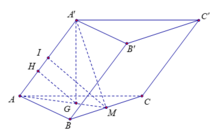
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)

Đáy ABC vuông cân tại B thì ACB=BAC=45\(^0\)chứ bạn.
Bạn có gõ nhầm đề không?

Chọn B
Ta có A ' G ⊥ A B C nên A ' G ⊥ B C ; B C ⊥ A M ⇒ B C ⊥ M A A '
Kẻ M I ⊥ A A ' ; B C ⊥ I M nên d A A ' ; B C = I M = a 3 4
Kẻ G H ⊥ A A ' , ta có
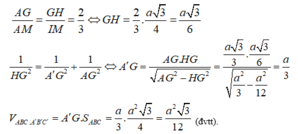

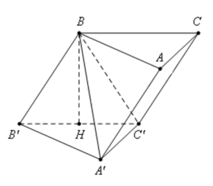


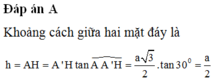
Ta có :![V_{E.HB'C'} = \frac{1}{3}.d[E,(A'B'C')].S_{C'HB'}](http://latex.codecogs.com/gif.latex?V_%7BE.HB%27C%27%7D&space;=&space;%5Cfrac%7B1%7D%7B3%7D.d%5BE,(A%27B%27C%27)%5D.S_%7BC%27HB%27%7D)
Do H là trung điểm của A'B' nên :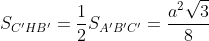
BE // (A'B'C') nên![d[E,(A'B'C')] = d[B,(A'B'C')] = BH](http://latex.codecogs.com/gif.latex?d%5BE,(A%27B%27C%27)%5D&space;=&space;d%5BB,(A%27B%27C%27)%5D&space;=&space;BH)
Trong tam giác vuông BB'H có :
Do đó :
+ Tính khoảng cách từ B đến mặt phẳng (AA'C'C).
Gọi M là điểm đối xứng của H qua A'. Khi đó)
Ta có![A' = B'M \cap (AA'C'C) \Rightarrow \frac{d[M,(AA'C'C)]}{d[B,(AA'CC)]} = \frac{A'M}{B'A'} = \frac{B'H}{B'A'}=\frac{1}{2}](http://latex.codecogs.com/gif.latex?A%27&space;=&space;B%27M&space;%5Ccap&space;(AA%27C%27C)&space;%5CRightarrow&space;%5Cfrac%7Bd%5BM,(AA%27C%27C)%5D%7D%7Bd%5BB,(AA%27CC)%5D%7D&space;=&space;%5Cfrac%7BA%27M%7D%7BB%27A%27%7D&space;=&space;%5Cfrac%7BB%27H%7D%7BB%27A%27%7D=%5Cfrac%7B1%7D%7B2%7D)
Trong) dựng
dựng  (Định lý 3 đường vuông góc)
(Định lý 3 đường vuông góc)
.)
,) dựng
dựng )
![\Rightarrow d[M, (AA'C'C)]= MK.](http://latex.codecogs.com/gif.latex?%5CRightarrow&space;d%5BM,&space;(AA%27C%27C)%5D=&space;MK.)
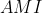 có :
có : 
 có
có &space;=&space;A%27H.%5Csin&space;(60%5E0).)
Trong
Xét tam giác vuông
Xét tam giác
hjjj
cop mạng nek