Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta tính thể tích hình chóp A’.BCB’. Gọi M là trung điểm của B’C’, ta có: ATM ⊥ B’C’ (1)
Lăng trụ ABC.A’B’C’ là lăng trụ đứng nên: BB’ ⊥ (A’B’C’) ⇒BB’⊥ A’M (2)
Từ (1) và (2) suy ra
AM⊥ (BB’C) hay A’M là đường cao của hình chóp A’.BCB’


Gọi E là trung điểm BC → AE vuông góc (vg) với BC
mà (ABC) vg (BB'C'C)
→ AE vg (BB'C'C)
\(V_{A.BB'C'C}=\frac{1}{3}\cdot AE\cdot S_{BB'C'C}=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\cdot BB'\cdot BC=\frac{a^3\sqrt{3}}{3}\)
Vì SBB'C = 1/2 * SBB'C'C
nên VABB'C' = 1/2 * VA.BB'C'C = (a3căn3)/6

Gọi I, K lần lượt là trung điểm của AB và A’B’, G là trọng tâm của tam giác ABC.Đường thẳng qua G, song song với AB cắt AC và BC lần lượt tại E và F, đường thẳng EF chính là giao tuyến của hai mặt phẳng (GA’B’) và (ABC).



\(V=2a.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=2a^3\sqrt{3}\)

Chọn C.
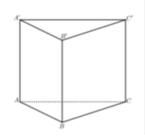
Gọi (H) là lăng trụ đứng tam giác đều ABC.A'B'C'
Ta có thể tích khối lăng trụ ABC.A'B'C' là:
V = A A ' . S A B C = a . a 2 3 4 = a 3 3 4

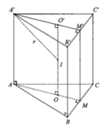
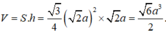
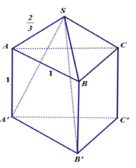
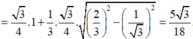
Ta chia khối lẳng trụ đã cho thành hình chóp A’.ABC, C.A’B’C’ và C.A’BB’
Ta có: VA’.ABC = VA’B’C’ =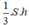 trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
trong đó S là diện tích đáy S = SABC = SA’B’C’ và h là chiều cao của hình lăng trụ
Lại có: VABC.A’B’C’ = S.h
Do đó,
Trong đó, tam giác ABC là tam giác đều có độ dài cạnh bằng a nên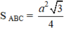
Vì đây là hình lăng trụ đứng nên h = AA’ = BB’= CC’ = a.
Vậy thể tích hình chóp C.A’BB’ là: