Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
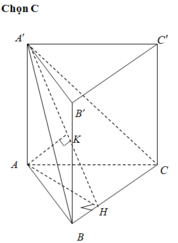
Gọi H là hình chiếu vuông góc của A lên BC.
Gọi K là hình chiếu vuông góc của A lên A’H.
Áp dụng định lí pytago vào tam giác vuông ABC ta tính được AB= a.
Gọi N là trung điểm A'B' \(\Rightarrow MN//AA'\Rightarrow N\in\left(P\right)\)
Trong mặt phẳng (A'B'C), gọi E là trung điểm A'C
\(\Rightarrow NE\) là đường trung bình tam giác A'B'C
\(\Rightarrow NE//B'C\) , mà \(N\in\left(P\right)\Rightarrow E\in\left(P\right)\)
Trong mặt phẳng (ACC'A'), qua E kẻ đường thẳng song song AA' cắt AC tại I
\(\Rightarrow IE\) là đường trung bình tam giác ACA'
\(\Rightarrow I\) là trung điểm AC hay \(\frac{IA}{IC}=1\)
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)
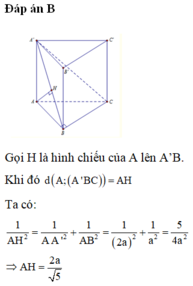
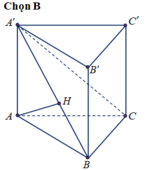
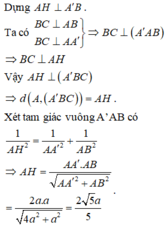
Chọn B.
- Tam giác ABC vuông cân tại A, BC = 42cm
- Tứ diện A.A’BC là tứ diện vuông tại A. Gọi h = d( A, (A’BC)), ta có: