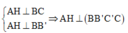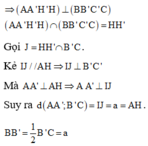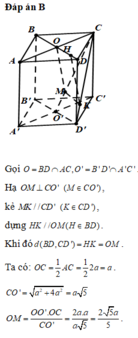Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

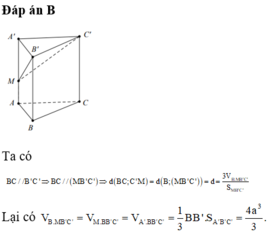
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)

Chọn A.
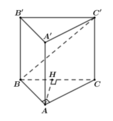
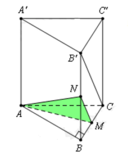
Gọi H là hình chiếu của A lên BC. Ta có
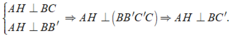
Suy ra AH là đoạn vuông góc chung của AA' và BC' nên
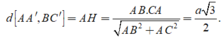

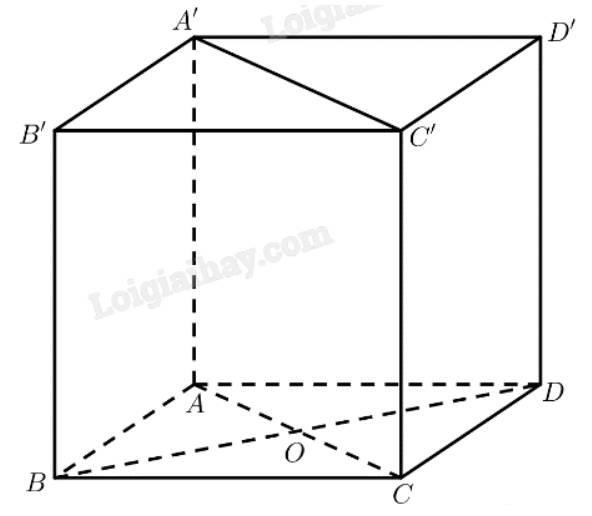
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)