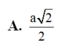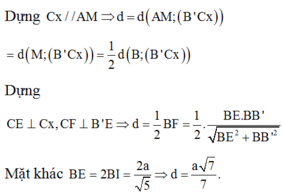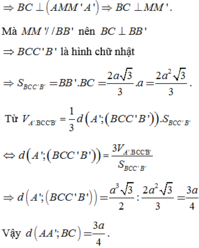Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
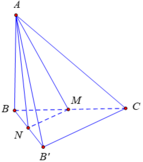
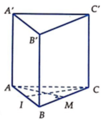
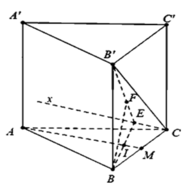
Tam giác ABC vuông và AB=BC=a nên ΔABC chỉ có thể vuông tại B.
Ta có A B ⊥ B C A B ⊥ B B ' ⇒ A B ⊥ B C B '
Kẻ 
⇒ d = d B ' C , M N = d B ' C , A M N = d C , A M N = d B , A M N
Tứ diện BAMN là tứ diện vuông
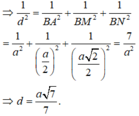
Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằng
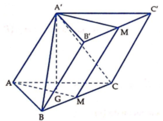
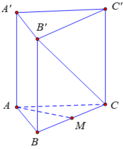
Do A' cách đều A; B; C \(\Rightarrow\) hình chiếu vuông góc H của A' lên (ABC) trùng tâm của tam giác ABC
\(\Rightarrow\widehat{A'AH}=60^0\)
\(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow AA'=\dfrac{AH}{cos60^0}=\dfrac{2a\sqrt{3}}{3}=BB'=CC'=A'B=A'C\) (do A' cách đều A, B, C nên \(A'A=A'B=A'C\))
Ta có: \(\left\{{}\begin{matrix}A'H\perp\left(ABC\right)\Rightarrow A'H\perp BC\\AH\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(A'AH\right)\Rightarrow BC\perp AA'\)
\(\Rightarrow BC\perp BB'\Rightarrow B'C'CB\) là hình chữ nhật (hình bình hành có 1 góc vuông)
\(S_{BCC'B'}=BB'.BC=\dfrac{2a^2\sqrt{3}}{3}\)
Gọi M là trung điểm AB \(\Rightarrow A'M=\sqrt{A'A^2-\left(\dfrac{AB}{2}\right)^2}=\dfrac{a\sqrt[]{39}}{6}\)
\(S_{A'AB}=\dfrac{1}{2}A'M.AB=\dfrac{a^2\sqrt{39}}{12}\)
\(\Rightarrow S_{xq}=S_{BCC'B'}+4S_{A'AB}=...\)