Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự 1A
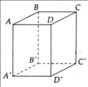
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')

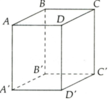
a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.

a. Ta có: AB // CD và AB = CD
CD // C1D1 và CD = C1D1
Suy ra: AB // C1D1 và AB = A1D1
Vì tứ giác ABC1D1 là hình bình hành nên AC1 và BD1 cắt nhau (hai đường chéo cắt nhau)
b. Vì các điểm A, C, C1 và A1 cùng thuộc mp(ACC1A1) mà ACC1A1 là một hình chữ nhật nên AC1 cắt A1C.
c. Vì BD1 không thuộc mp(ADD1A1), không thuộc mp(ABB1A1) và cũng không thuộc mp(ACC1A1) nên BD1 và AA1 không cắt nhau.

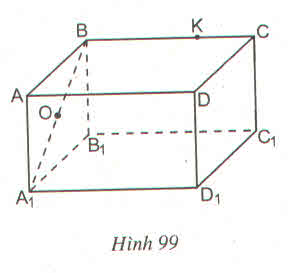
A B C D O K a)Xét tứ giác OBKC, ta có:
OC//BK(BK//AC)
BO//KC(KC//BD)
=>tứ giác OBKC là hình bình hành
lại có:
AC \(\perp\) BD ( hai đường chéo)
BD//KC
=> \(\)góc OCK =90o
=> hình bình hành OBKC là hình chữ nhật
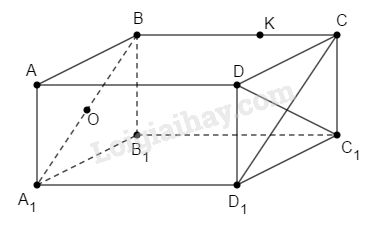
b)Ta có:
BC = OK ( do OCKD là hình chữ nhật)
AB=BC( cách cạnh hình thoi bằng nhau)
=> AB = OK
c)
* nếu tứ giác ABCD là hình vuông:
=>BD=AC
mà: BO=1/2BD
OC=1/2AC
=> BO = OC
=> hình chữ nhật OBKC là hình vuông.
Vậy HCN OBKC là hình vuông khi hình thoi ABCD là hình vuông


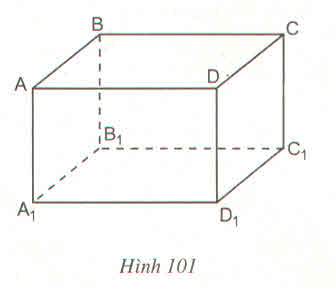

a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').