Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

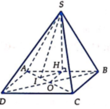
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

Đáp án D.
Phương pháp giải: Dựng hình để xác định góc giữa hai đường thẳng chéo nhau: Góc giữa hai đường thẳng a và b là góc giữa a’ và b với a // a’.
Lời giải: Vì ABCD là hình vuông ⇒ A C ⊥ B D mà A C / / A ' C ' ⇒ A ' C ' ⊥ B D

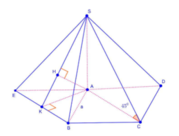
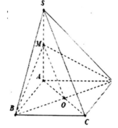
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
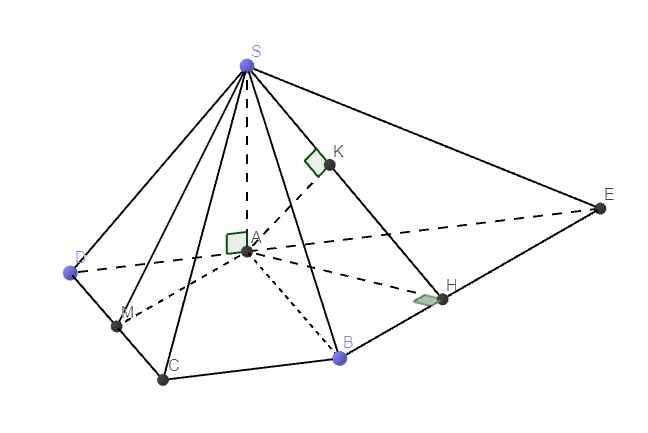
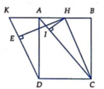
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Chọn A.
Góc giữa SC và mặt đáy bằng 45 o ⇒ S C A ^ = 45 o
Xét tam giác SAC vuông tại A, ta có
![]()
Dựng hình bình hành ACBE
![]()
Gọi H là hình chiếu của A lên mặt phẳng (SBE).
![]()
![]()
Xét hình tứ diện vuông SABE có
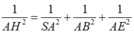
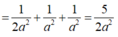
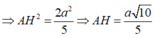

Đáp án D
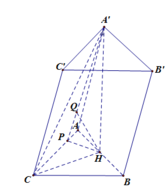
Ta có các tam giác SAB, SAD, SAC là các tam giác vuông tại A
Nên S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ ( A B C D )
Gọi O = A C ∩ B D và M là trung điểm của SA.
Do đó OM//SC
Hay SC// (MBD) nên
![]()
Có B M = A M 2 + A B 2 = a 7 2
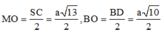
Áp dụng định lý cosin trong tam giác MOB, ta được
![]()
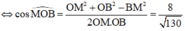
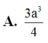
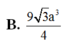
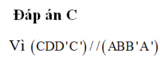

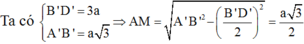
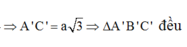

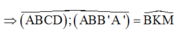

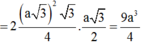
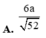

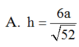
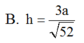
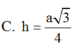
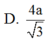

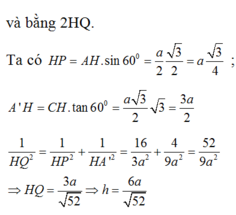
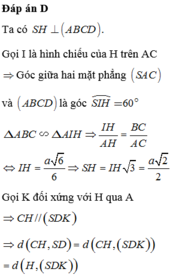

Đáp án A.