Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần I hôm qua mình trl rồi .
Phần II
Câu 1: Chỉ ra các phương thức biểu đạt chính của văn bản?
Các PTBĐ : Tự sự , miêu tả , biểu cảm .
Câu 2: Kể tên ít nhất 2 truyện cổ hoặc 2 câu ca dao được gợi nhớ trong khổ thơ 1 và 2.
- 2 truyện cổ tích được gợi nhớ trong khổ 1 & 2 :
+ Tấm cám .
+ Sự tích cây Khế.

\(2tan^2x-2\sqrt{3}tanx-3=0\)
\(\orbr{\begin{cases}tanx=\frac{3+\sqrt{3}}{2}\\tanx=\frac{-3+\sqrt{3}}{2}\end{cases}}\)
\(\orbr{\begin{cases}tanx=tana\\tanx=tanb\end{cases}}\) Đặt \(tana=\frac{3+\sqrt{3}}{2};tanb=\frac{-3+\sqrt{3}}{2}\)
\(\orbr{\begin{cases}x=a+k\pi\\x=b+k\pi\end{cases};k\in Z}\)
\(\sqrt{3}cot^2x-\left(1+\sqrt{3}\right)cotx+1=0\)
\(\orbr{\begin{cases}cotx=1\\cotx=\frac{\sqrt{3}}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tanx=1=tan\frac{\pi}{4}\\tanx=\sqrt{3}=tan\frac{\pi}{3}\end{cases}}\)
\(\orbr{\begin{cases}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{3}+k\pi\end{cases};k\in Z}\)

1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+=???
Phép tính như thế thì mời nhà toán hok về lm giùm!
KO NÊN ĐĂNG CÂU HỎI LINH TINH!
#Biinz_Tổng's
#Dương_Hoàng_Anh
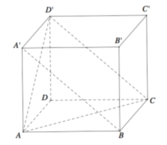
Đáp án A
Chọn gốc tọa độ tại D, các tia Ox, Oy, Oz trùng với các tia DC,DA,DD'.
Và B(1;2;0)
Do đó