


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




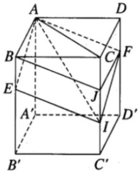
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.
Từ đó suy ra IJ = EB = DF = JC = c/3
Ta có
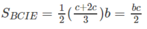
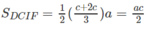
Nên V H = V A . BCIE + V A . DCIF
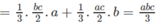
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên
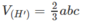
Từ đó suy ra 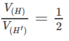

b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

Đáp án D
Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Dễ thấy MN đi qua B, các hình chóp E.AMB và F.CNB có diện tích đáy và chiều cao bằng nhau. Áp dụng công thức (7) ta có:
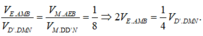
Áp dụng ví dụ 9, ta có:
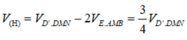
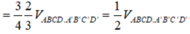
Suy ra V(H) = V(H'). Do đó k = 1.

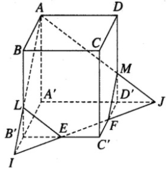
Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M. Gọi V0 là thể tích khối tứ diện AA’IJ. V là thể tích khối hộp ABCD.A’B’C’D’
Vì EB’ = EC’ và B’I // C’F
nên IB′ = FC′ = 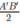
Do đó 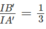
Để ý rằng BE’ // A’J , B’L // AA’
Ta có
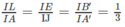
Từ đó suy ra:
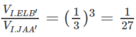
Do đó 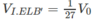
Tương tự 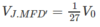
Gọi AB = a, BC = b , đường cao hạ từ A xuống (A’B’C’D’) là h thì
V = V ABCD . A ' B ' C ' D ' = h a b . sin ∠ BAD
![]()
Vậy
![]()
![]()
![]()

Trước hết, ta xác định thiết diện của hình hộp ABCD.A’B’C’D’ khi cắt bởi mp (CEF). Mặt phẳng (CEF) chứa đường thẳng EF mà E là trung điểm của BB’, F là trung điểm của cơ nên EF chứa giao điểm O của các đường chéo hình hộp, do đó mặt phẳng (CEF) cùng chứa giao điểm O của các đường chéo và nó cũng chứa đường chéo A’C của hình hộp. Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành CEA’F. Qua EF ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt AA’ ở p và cắt CC’ ở Q.
ta có thể tích của hình hộp ABCD.PEQF là: VABCD.PEQF =1/2 VABCD.A’B’C’D’ (1)
Ta cũng chứng minh được một cách dễ dàng: VCFQE = VA’FPE (2) (Hai hình chóp CFQE và A’FPE có chiều cao bằng nhau và diện tích đáy bằng nhau).
Xét khối đa diện ABCDE’F do mặt phẳng (CEF) chia ra trên hình hộp p ABCD.A’B’C’D ta có: VABCD.FA’EQ = VABCD.FPE +VA’FPE (3)
Từ (1), (2), (3) suy ra: VABCD.FA’EQ = 1/2 VABCD.A’B’C’D’ Vậy mặt phẳng (CEF) chia hình hộp thành hai khối đa diện có thể tích bằng nhau, tỉ số của chúng là 1. Chú ý: Có thể lí luận như sau: Giao điểm O của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng (CEF) chứa điểm o nên chia hình hộp thành hai hình đối xứng với nhau qua điểm o. Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.

Chọn D.
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H