Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

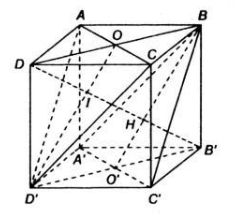
ABB'A' và CDD'C' là hình vuông \(\Rightarrow CD'\perp DC'\Rightarrow CD'\perp\left(ADC'B'\right)\)
Gọi M là giao điểm CD' và DC' \(\Rightarrow\) M là trung điểm 2 đoạn nói trên
Trong mp (ADC'B'), từ M kẻ \(MH\perp AC'\Rightarrow MH\) là đường vuông góc chung của AC' và CD'
\(DC'=AB'=\sqrt{AB^2+A'A^2}=a\sqrt{2}\)
\(\Rightarrow AD=B'C'=\sqrt{AC'^2-AB'^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ADC'\) vuông cân tại D \(\Rightarrow\Delta MHC'\) vuông cân tại H
\(\Rightarrow MH=\dfrac{MC'}{\sqrt{2}}=\dfrac{DC'}{2\sqrt{2}}=\dfrac{a}{2}\)


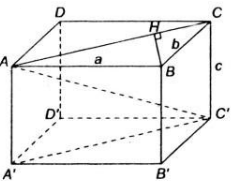
b) Xét tứ giác A’BCD’ có BC//A’D’ và BC = A’D’
=> tứ giác A’BCD’ là hình bình hành
=> BA’ // CD’ ( tính chất của hình bình hành)
Tương tự, tứ giác ABC’D’ là hình bình hành nên BC’//AD’
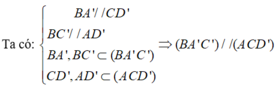
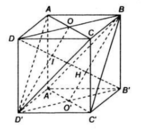
Gọi O và O’ là tâm của ABCD và A’B’C’D’.
Gọi H và I lần lượt là tâm của hai tam giác đều BA’C’ và ACD’.
* Xét ( BB’D’D) có BO’// D’O nên OI // HB
Lại có: O là trung điểm BD
=> I là trung điểm của HD: IH = ID (1)
* Xét (BB’D’D) có D’O// BO’ nên D’I // HO’
Lại có: O’ là trung điểm của B’D’ nên H là trung điểm B’I: HI = HB’ (2)
Từ (1) và (2) suy ra: 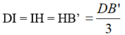
* Theo phần trên B'D ⊥ (BA'C) ⇒ IH ⊥ (BA'C)
Mà I ∈ (ACD') nên khoảng cách giữa hai mp song song (ACD’) và ( BA’C’) là độ dài đoạn IH.
Khi đó:
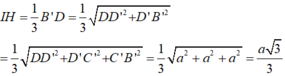
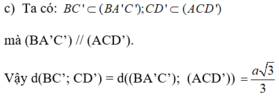

a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)

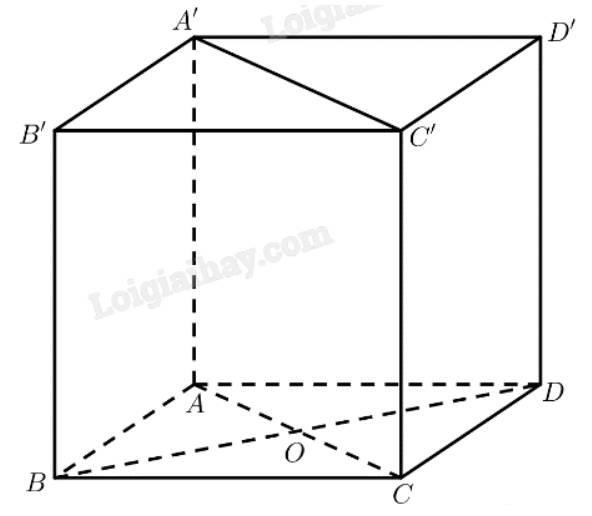
a) Gọi E là trung điểm của AD
\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)
Mà tam giác SAD đều
\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)
Xét tam giác SDE vuông tại E có
\(SE = \sqrt {S{D^2} - D{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)
Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)
\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a
c) Trong (SAD) kẻ \(AF \bot SD\)
Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)
\( \Rightarrow \) d(AB, SD) = AF
Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)
Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)

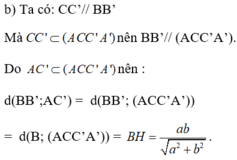



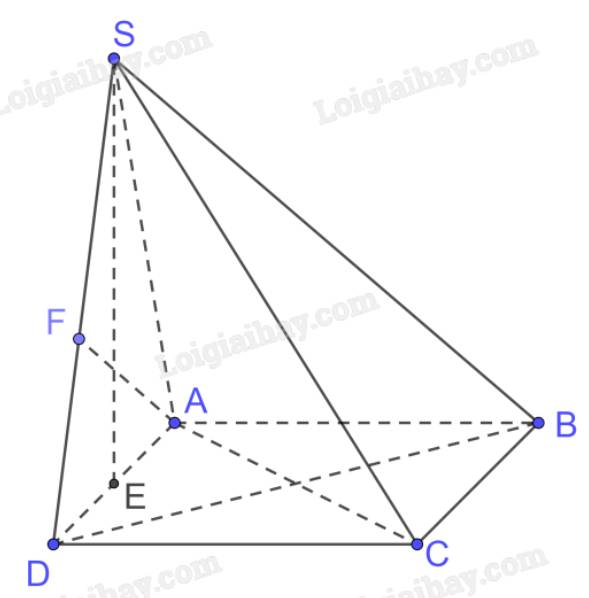
a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB'\left( {BB' \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB'D'D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B'D' \subset \left( {A'B'C'D'} \right),\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\)
\( \Rightarrow d\left( {AC,B'D'} \right) = d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = BB' = a\)