Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sxq=(12+9)*2*10=20*21=420cm2
Sxq=420+2*12*9=636cm2
V=12*9*10=1080cm3
b: Xét tứ giác BIFO có
BI//FO
BI=FO
=>BIFO là hình bình hành
=>IO//BF//DH
=>IO//(BFGC); IO//(AEHD)

a) Xét ΔABC có
E là trung điểm của AB(gt)
F là trung điểm của BC(gt)
Do đó: EF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒EF//AC và \(EF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔADC có
H là trung điểm của AD(gt)
G là trung điểm của CD(gt)
Do đó: HG là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra HG//EF và HG=EF
Xét ΔABD có
E là trung điểm của AB(gt)
H là trung điểm của AD(gt)
Do đó: EH là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒EH//BD và \(EH=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: EH//BD(cmt)
BD⊥AC(gt)
Do đó: EH⊥AC(Định lí 2 từ vuông góc tới song song)
Ta có: HG//AC(cmt)
EH⊥AC(Cmt)
Do đó: HG⊥HE(Định lí 2 từ vuông góc tới song song)
hay \(\widehat{EHG}=90^0\)
Xét tứ giác EHGF có
HG//EF(cmt)
HG=FE(cmt)
Do đó: EHGF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành EHGF có \(\widehat{EHG}=90^0\)(cmt)
nên EHGF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: EFGH là hình chữ nhật(cmt)
nên \(S_{EFGH}=EF\cdot EH\)
\(\Leftrightarrow S_{EFGH}=\dfrac{AC}{2}\cdot\dfrac{BD}{2}=\dfrac{10}{2}\cdot\dfrac{8}{2}=5\cdot4=20cm^2\)
Vậy: Diện tích tứ giác EFGH khi AC=10cm và BD=8cm là 20cm2
c) Hình chữ nhật EFGH trở thành hình vuông khi EH=HG
hay AC=BD
Vậy: Khi tứ giác ABCD có thêm điều kiện AC=BD thì EFGH trở thành hình vuông

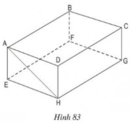
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

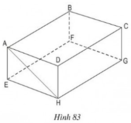
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).