Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
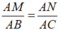
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)

Đặt \(\overrightarrow{AB}=\overrightarrow{a}\) , \(\overrightarrow{AC}=\overrightarrow{b}\) và \(\overrightarrow{AA'}=\overrightarrow{c}\) khi đó
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{a}+\frac{1}{2}.\overrightarrow{c}\)
\(\overrightarrow{AN}=\overrightarrow{AA'}+\overrightarrow{A'N}=\frac{1}{2}.\overrightarrow{b}+\overrightarrow{c}\)
\(\overrightarrow{AP}=\overrightarrow{AB}'+\overrightarrow{B'P}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}.\overrightarrow{b}+\overrightarrow{c}\)
Do \(c\frac{2}{3}.\overrightarrow{a}+\frac{1}{3}.\overrightarrow{b}+\overrightarrow{c}=\frac{2}{3}\left(\overrightarrow{a}+\frac{1}{2}.\overrightarrow{c}\right)+\frac{2}{3}\left(\frac{1}{2}.\overrightarrow{b}+\overrightarrow{c}\right)\)
Nên \(3\overrightarrow{AP}=2\overrightarrow{AM}+2\overrightarrow{AN}\)
Suy ra A, M, N, P đồng phẳng

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

A' A B' D' C' B C D M N O' O
Đặt \(\overrightarrow{AA'}=\overrightarrow{a}\), \(\overrightarrow{AB'}=\overrightarrow{b}\) và \(\overrightarrow{AD}=\overrightarrow{d}\)
Theo quy tắc hình bình hành ta có :
\(\overrightarrow{AC'}=\overrightarrow{AA'}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{d}\)
Mà \(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{d}=\overrightarrow{AA'}+\overrightarrow{AB}+\overrightarrow{AD}=3\overrightarrow{AM}\)
Suy ra \(\overrightarrow{AC'}=3\overrightarrow{AM}\)
Do đó A, M, C' thẳng hàng
Tương tự cũng có C', N, A thẳng hàng. Suy ra điều cần chứng minh
Do \(\frac{BM}{MB'}=\frac{CN}{ND}\) nên \(\frac{BM}{BB'}=\frac{CN}{CD}=t\) với \(t\in\left(0;1\right)\) nào đó
Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AD}=\overrightarrow{b}\) và \(\overrightarrow{AA'}=\overrightarrow{c}\)
Khi đó :
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{a}+t\overrightarrow{c}\)
\(\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=\left(1-t\right)\overrightarrow{a}+\overrightarrow{b}\)
\(\overrightarrow{AI}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
\(=\overrightarrow{AA'}+\overrightarrow{A'J}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}\)
Suy ra :
\(\overrightarrow{MN}=-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}\) ; \(\overrightarrow{MI}=\frac{1}{2}\overrightarrow{b}-t\overrightarrow{c}\) và \(\overrightarrow{MJ}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Từ đó, do
\(-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}=\left(2-t\right).\left(\frac{1}{2}.\overrightarrow{b}-t.\overrightarrow{c}\right)+t.\left(-\overrightarrow{a}\right)+\frac{1}{2}.\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Nên :
\(\overrightarrow{MN}=\left(2-t\right).\overrightarrow{MI}+t.\overrightarrow{MJ}\)
Suy ra M, N, I, J đồng phẳng
B' A' D' C' B A C D N I M J