Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

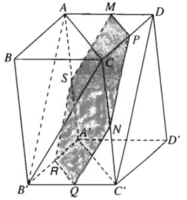
a) Vẽ MP song song với AC và cắt CD tại P
Ta có: 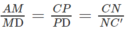
Do đó PN // DC′ // AB′
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có MP // AC và PN // AB′. Vậy mặt phẳng(MNP) song song với mặt phẳng (ACB’) và do đó MN // (ACB′)
b) Vì mặt phẳng (MNP) song song với mặt phẳng (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ NQ // CB′, QR // C′A′ ((// CA), RS //AB′ (//PN) và tất nhiên SM // QN. Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: MP // RQ, PN //SR, NQ // MS.

\(\frac{SM}{MC}=\frac{SN}{ND}\Rightarrow MN//CD\) theo Talet đảo

C' C B N B' D' A' A D M b a
Đặt \(\overrightarrow{AB}=\overrightarrow{a}\) , \(\overrightarrow{AD}=\overrightarrow{b}\) ,\(\overrightarrow{AA'}=\overrightarrow{c}\)
Với \(\begin{cases}\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=1\\\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\end{cases}\)
Suy ra \(\overrightarrow{A'C}=\overrightarrow{AC}-\overrightarrow{AA'}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\)
Từ giả thiết suy ra \(\frac{AM}{AD}=\frac{B'N}{B'B}\)
Do đó
\(\overrightarrow{AM}=k.\overrightarrow{b}\) , \(\overrightarrow{AN}=\overrightarrow{a}+\left(1-k\right).\overrightarrow{c}\)
Ở đây, \(k=\frac{AM}{AD}=\frac{B'N}{B'B}\)
Suy ra :
\(\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{a}-k.\overrightarrow{b}+\left(1-k\right).\overrightarrow{c}\)
Khi đó :
\(\overrightarrow{MN}.\overrightarrow{A'C}=\left(\overrightarrow{a}-k.\overrightarrow{b}+\left(1-k\right).\overrightarrow{c}\right).\left(\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\right)\)
\(=1-k+k-1=0\)
Do đó : \(MN\perp A'C\)

Do \(A'B'//CD\Rightarrow A'\in\left(CDB'\right)\)
Gọi E, F lần lượt là trung điểm BC và AD \(\Rightarrow EF//CD\Rightarrow EF\in\left(P\right)\) do EF qua N
Gọi P là trung điểm BB' \(\Rightarrow EP//B'C\) (đường trung bình) \(\Rightarrow P\in\left(P\right)\)
Gọi Q là trung điểm AA' \(\Rightarrow QF//A'D\Rightarrow Q\in\left(P\right)\)
Trong mp (ABB'A'), nối AB' cắt PQ tại M
\(\Rightarrow\) M là trung điểm AB' theo t/c hình bình hành
\(\Rightarrow AM=\frac{1}{2}AB'=\frac{1}{2}DC'\Rightarrow\frac{AM}{DC'}=\frac{1}{2}\)

Câu hỏi của Julian Edward - Toán lớp 11 | Học trực tuyến

