Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)

Đáp án B và D giống nhau nên chắc chắn cả 2 đều đúng
Kiểm tra 2 đáp án A và C:
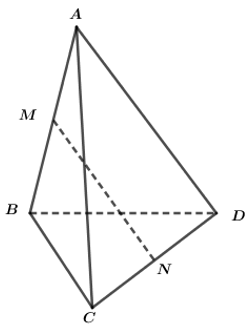
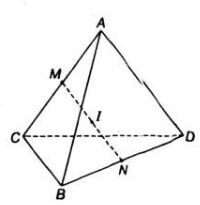
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{MD}\right)=\frac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\)
Vậy đáp án A đúng nên đáp án C sai

Do phép vị tự tỉ số k biên \(\overrightarrow{u}\) thành \(\overrightarrow{v}\Rightarrow\overrightarrow{v}=k\overrightarrow{u}\)
\(\Leftrightarrow\left(-1;-4\right)=k\left(2;8\right)\Rightarrow\left\{{}\begin{matrix}-1=2k\\-4=8k\end{matrix}\right.\)
\(\Rightarrow k=-\frac{1}{2}\)

\(\overrightarrow{u}^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=2a^2-2a^2.cos60^0=a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=a\)
\(\overrightarrow{a}.\overrightarrow{u}=\overrightarrow{a}\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2-\overrightarrow{a}.\overrightarrow{b}=a^2-a^2.cos60^0=\frac{a^2}{2}\)
\(\Rightarrow cos\left(\overrightarrow{a};\overrightarrow{u}\right)=\frac{\overrightarrow{a}.\overrightarrow{u}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{u}\right|}=\frac{a^2}{2a^2}=\frac{1}{2}\Rightarrow\left(\overrightarrow{a};\overrightarrow{u}\right)=60^0\)

1.
Do \(\overrightarrow{v}\) cùng phương với \(\overrightarrow{u}\) nên \(\overrightarrow{v}=\left(a;a\right)\) với a là số thực khác 0
Chọn \(M\left(0;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=a+0=a\\y_{M'}=a+0=a\end{matrix}\right.\) \(\Rightarrow M'\left(a;a\right)\)
Thay vào pt d' ta được:
\(a+a-4=0\Rightarrow a=2\)
\(\Rightarrow\overrightarrow{v}=\left(2;2\right)\)
\(\Rightarrow\left|\overrightarrow{v}\right|=2\sqrt{2}\)
2.
Gọi \(\overrightarrow{u}=\left(a;b\right)\)
Gọi \(A\left(0;1\right)\) là 1 điểm thuộc d
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{u}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=a\\y_{A'}=b+1\end{matrix}\right.\)
Thay tọa độ A' vào pt d' ta được: \(a+b+1-5=0\Leftrightarrow a+b=4\)
Ta có:
\(\left|\overrightarrow{u}\right|=\sqrt{a^2+b^2}\ge\sqrt{\frac{1}{2}\left(a+b\right)^2}=2\sqrt{2}\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=2\sqrt{2}\) khi \(a=b=2\)


D
\(\overrightarrow{AC'}+\overrightarrow{CA'}+\overrightarrow{BD'}+\overrightarrow{DB'}\)
\(=2\left(\overrightarrow{OC'}+\overrightarrow{OA'}\right)+2\left(\overrightarrow{OD'}+\overrightarrow{OB'}\right)\)
\(=2.\left(-2\overrightarrow{OI}\right)+2.\left(-2\overrightarrow{OI}\right)\)
\(=-4.2\overrightarrow{OI}\)
\(\Rightarrow2\overrightarrow{OI}=-\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)