

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




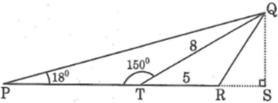
Kẻ QS⊥PR
Ta có : \(\widehat{QTS}=180^0-\widehat{QTP}=180^0-150^0=30^0\)
Trong tam giác vuông QST, ta có:
\(QS=QT.sinQTS=8.sin30^0=4\left(cm\right)\)
\(TS=QT.cosQTS=8.cos30^0\sim6,928\left(cm\right)\)
Trong tam giác vuông QSP, ta có:
\(SP=QS.cotQPS=4.cot18^0=12,311\left(cm\right)\)
\(PT=SP-TS\sim12,311-6,928\sim5,383\left(cm\right)\)
b) Ta có:
\(S_{QPR}=\frac{1}{2}.QS.PR=\frac{1}{2}.QS.\left(PT+TR\right)\sim\frac{1}{2}.4.\left(5,383+5\right)\sim20,766\left(cm^2\right)\)

Bài 1:
a: ĐKXĐ: x>0; x<>1
b: \(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)\cdot\left(1+\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{2}{\sqrt{x}-1}\)
c: Thay \(x=6+2\sqrt{5}\) vào A, ta được:
\(A=\dfrac{2}{\sqrt{5}+1-1}=\dfrac{2\sqrt{5}}{5}\)
d: Để |A|>A thì A>0
=>\(\sqrt{x}-1>0\)
hay x>1

Nhầm:
\(\left\{\begin{matrix}2x+3y=m\\-5x+y=-1\end{matrix}\right.\)
(1) trừ (2) nhân (3)
\(x=\frac{m+3}{17}>0\Rightarrow m>-3\) (*)
thế vào (2)
\(y=5.\frac{m+3}{17}-1=\frac{5m+15-17}{17}=\frac{5m-2}{17}>0\Rightarrow m>\frac{2}{5}\) (**)
Từ (*) và (**) có m>2/5
gọi x, y (km/h) lần lượt là vận tốc của xe ô tô xuất phát từ A và B (x, y >0)
khi đó: + quãng đường xe ô tô xuất phát từ A đi được là 3x
+quãng đường xe ô tô xuất phát từ B đi được là 3y
nên ta có : 3x+3y=210 \(\Leftrightarrow\)x+y = 70 (1)
vì vận tốc của xe xuất phát từ A lớn hơn xe xuất phát B 10km/h nên ta có phương trình: x-y =10 (2)
từ (1) và (2) => ta có hệ phương trình :\(\left\{\begin{matrix}x+y=70\\x-y=10\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{\begin{matrix}2x=80\\x-y=10\end{matrix}\right.\Leftrightarrow\)\(\left\{\begin{matrix}x=40\\40-y=10\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{\begin{matrix}x=40\left(thỏa\right)\\y=30\left(thỏa\right)\end{matrix}\right.\)
vậy vận tốc của 2 xe ô tô lần lượt là 40 km/h và 30 km/h

thôi gợi ý :v dg chán đời lại mới coi xong anime, "Happy Ending" :v
By AM-GM have:
\(xy+xz+yz \ge 3\sqrt[3]{x^2y^2z^2} \)
\(\sqrt[3]{xyz} \le \sqrt{\dfrac{x^2+y^2+z^2}{3}} \)
\(x+y+z \le \sqrt{3(x^2+y^2+z^2)}\)
haizz vô dụng v~
\(\Rightarrow A \le \dfrac{\sqrt[3]{xyz}(x+y+z+\sqrt{x^2+y^2+z^2})}{3(x^2+y^2+z^2)} \)
\(\Rightarrow A \le \dfrac{\sqrt{\dfrac{x^2+y^2+z^2}{3}}(\sqrt{3(x^2+y ^2+z^2)}+\sqrt{x^2+y^2+z^2})}{3(x^2+y^2+z^2)}= \dfrac{3+\sqrt{3}}{9} \)