Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)

Bài làm
a) Ta có: DE // AB ( gt )
=> DE // FA
=> \(\widehat{DEF}=\widehat{AFE}\)( Hai góc so le trong )
Lại có: DF // AC ( gt )
=> DF // AE
=> \(\widehat{DFE}=\widehat{AEF}\)( Hai góc so le trong )
Xét tam giác AEF và tam giác DFE có:
\(\widehat{DEF}=\widehat{AFE}\)( cmt )
Cạnh chung: FE
\(\widehat{DFE}=\widehat{AEF}\) ( cmt )
=> Tam giác AEF = tam giác DFE ( g.c.g )
b) Xét tam giác DEC có:
\(\widehat{ABC}=\widehat{EDC}\)( do DE // AB và hai góc đó đồng vị )
Mà \(\widehat{ABC}=\widehat{ACB}\)( tam giác ABC cân )
=> \(\widehat{EDC}=\widehat{EDC}\)
=> Tam giác EDC cân tại E
=> DE = EC
Ta có: AF + FB = AB
hay DE + FB = 3,5
=> DE = 3,5 - FB (1)
Lại có: AE + EC = AC
hay FD + EC = 3,5
=> FD = 3,5 - EC (2)
Cộng (1) vào (2) ta được:
DE + FD = 3,5 - FB + 3,5 - EC
=> ED + FD = ( 3,5 + 3,5 ) - ( FB + EC )
hay ED + FD = 7 - ( FB + ED )
Mà DE = FA ( do tam giác AFE = tam giác DEF )
=> ED + FD = 7 - ( FB + FA )
hay ED + FD = 7 - AB
=> ED + FD = 7 - 3,5
=> ED + FD = 3,5 ( cm )
Vậy ED + FD = 3,5 cm
# Học tốt #

a) Ta có DE // AB, DF // AC, EF // BC. Vì EF // BC và DE // AB, theo định lí Thales, ta có:AB/BC = DE/EF. (1)Vì EF // BC và DF // AC, theo định lí Thales, ta có:AC/BC = DF/EF. (2)Từ (1) và (2), ta có:AB/BC = DE/EF = AC/BCRút gọn phương trình, ta được:AB = AC = BCVậy tam giác ABC = tam giác CEA.b) Vì AB = AC và DE // AB, theo định lí Thales, ta có:AB/DE = AC/CEVì vậy, AB = AC phải bao hàm DE = CE.c) Vì AB = BC và DE // AB, theo định lí Thales, ta có:AB/DE = BC/AEVì vậy, AB = BC phải suy ra DE = AE.d) Để chứng minh trung điểm 2 đoạn AC và BE trùng nhau, ta cần chứng minh rằng AE = EC và BD = DC.Vì DE // AB và DE = AE, theo định lí Thales, ta có:AB/DE = BC/ECVì thế,

a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>DB=DC
=>D là trung điểm của BC
c: ΔABC cân tại A
mà AD là trung tuyến
nên AD vuông góc BC
d: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
e: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
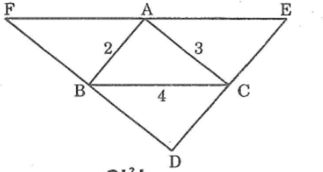
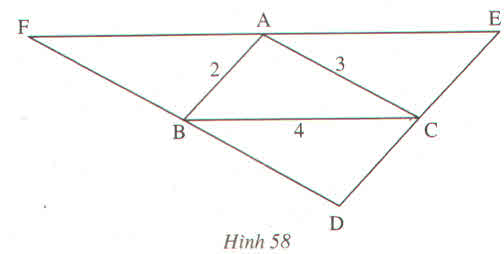



Xét ΔABC và ΔABF, ta có:
∠(ABC) =∠(BAF) (so le trong)
AB cạnh chung
∠(BAC) =∠(ABF) (so le trong)
Suy ra: ΔABC= ΔBAF(g.c.g)
Suy ra: AF = BC = 4 (hai cạnh tương ứng)
BF = AC = 3(hai cạnh tương ứng)
Xét ΔABC và ΔCEA, ta có:
∠(ACB) =∠(CAE) (so le trong)
AC cạnh chung
∠(BAC) =∠(ECA) (so le trong)
Suy ra: ΔABC= ΔCEA(g.c.g)
Suy ra: AE = BC = 4(hai cạnh tương ứng)
CE = AB = 2 (hai cạnh tương ứng)
Xét ΔABC và ΔDCB, ta có:
∠(ACB) =∠(DBC) (so le trong)
BC cạnh chung
∠(ABC) =∠(DCB) (so le trong)
Suy ra: ΔABC= ΔDCB(g.c.g)
Suy ra: DC = AB = 2(hai cạnh tương ứng)
DB = AC = 3 (hai cạnh tương ứng)
Ta có: EF = AE + AF = 4 + 4=8
DF = DB + BF = 3+ 3 =6
DE = DC + CE = 2 + 2 = 4
Vậy chu vi ΔDEF là:
DE + DF + EF = 4+ 6 + 8 =18 (đơn vị độ dài)