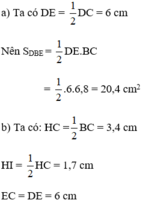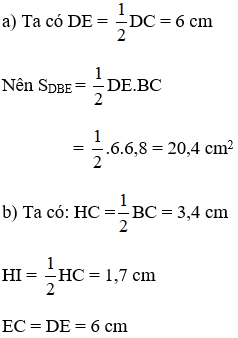Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

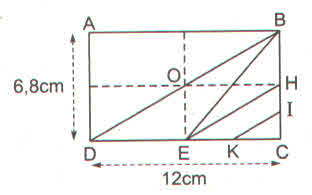
a)Ta có: DE=12DC(=12.12=6(cm)DE=12DC(=12.12=6(cm)
Nên SDBE=12.DE.BC=12.6.6,8=20,4(cm3)SDBE=12.DE.BC=12.6.6,8=20,4(cm3)
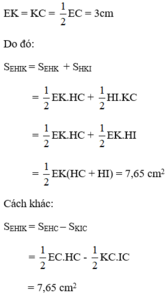
b)Ta có : HC=12BC=12.6,8=3,4(cm)HC=12BC=12.6,8=3,4(cm)
HI=12HC=12.3,4=1,7(cm)HI=12HC=12.3,4=1,7(cm)
EC = DE = 6cm
EK=KC=12EC=12.6=3(cm)EK=KC=12EC=12.6=3(cm)
Do đó SEHIK=SEHK+SHKI=12EK.HC+12HI.KCSEHIK=SEHK+SHKI=12EK.HC+12HI.KC
= 12EK.HC+12EK.HI=12EK(HC+HI)12EK.HC+12EK.HI=12EK(HC+HI)
SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)
Cách khác:
SEHIK=SEHC−SKIC=12EC.HC−12KC.ICSEHIK=SEHC−SKIC=12EC.HC−12KC.IC
= 12.6.3,4−12.3.1,712.6.3,4−12.3.1,7
= 10,2−2,55=7,65(cm2)

a: Xét tứ giác AKCQ có
AK//CQ
AK=CQ
Do đó: AKCQ là hình bình hành

Bài 2 :
D C A B H O E F G x y
Các tia đối Ox,Oy cắt CD, DAtheo thứ tự G, H
Do t/c đối xứng nên diện tích tứ giác OEBF = dt tứ giác OFCG = dt tứ giác OGDH= dt tứ giác OHAE
Mà tổng diện tích 4 tứ giác đó = dt hình vuông ABCD = a2
=> Diện tích tứ giác OEBF = \(\frac{a^2}{4}\)