Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

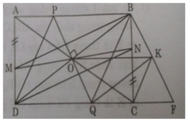
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.

a. Tứ giác ABCD là hình bình hành.
\(\Rightarrow AB=CD\)(tính chất hình bình hành)
và \(AB//CD\Rightarrow\widehat{ABD}=\widehat{BDC}\)(so le trong)
Xét \(\Delta AMB\)và \(\Delta CND\)có:
\(AB=CD\)(cmt)
\(\widehat{ABM}=\widehat{CDN}\)(cmt)
\(BM=DN\)(GT)
\(\Rightarrow\Delta AMB=\Delta CND\left(c.g.c\right)\)
b. Có AC cắt BD tại O
=> O là trung điểm của AC => OA = OC.
=> O là trung điểm của BD => OB = OD.
Có OB = OM + MD
OD = ON + ND
mà OB = OD, MB = ND
=> OM = ON => O là trung điểm của MN.
Trong tứ giác AMCN có:
OA = OC, OM = ON
=> Tứ giác AMCN có 2 đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

a: Xét tứ giác BMDN có
O là trung điểm của MN
O là trung điểm của BD
Do đó: BMDN là hình bình hành

a: Ta có: AM+MB=AB
CP+PD=CD
AQ+QD=AD
CN+NB=CB
mà AM=CP=AQ=CN và AB=CD=AD=CB
nên MB=PD=QD=NB
Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
b: ABCD là hình thoi
=>AC⊥BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác BNDQ có
BN//DQ
BN=DQ
Do đó: BNDQ là hình bình hành
=>BD cắt NQ tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của NQ
=>N,O,Q thẳng hàng
c: AMCP là hình bình hành
=>AC cắt MP tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MP
ΔAMQ cân tại A
=>\(\hat{AMQ}=\frac{180^0-\hat{MAQ}}{2}=\frac{180^0-\hat{BAD}}{2}\left(1\right)\)
ΔABD cân tại A
=>\(\hat{ABD}=\frac{180^0-\hat{BAD}}{2}\left(2\right)\)
Từ (1),(2) suy ra \(\hat{AMQ}=\hat{ABD}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên MQ//BD
Ta có: DQ=DP
=>ΔDQP cân tại D
=>\(\hat{DQP}=\frac{180^0-\hat{QDP}}{2}=\frac{180^0-\hat{ADC}}{2}\left(3\right)\)
ΔDAC cân tại D
=>\(\hat{DAC}=\frac{180^0-\hat{ADC}}{2}\left(4\right)\)
Từ (3),(4) suy ra \(\hat{DQP}=\hat{DAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên PQ//AC
mà AC⊥BD
nên PQ⊥BD
Ta có: PQ⊥BD
QM//BD
DO đó: QM⊥QP
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
=>MNPQ là hình bình hành
Hình bình hành MNPQ có QM⊥QP
nên MNPQ là hình chữ nhật