Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Để chứng minh BD = 2AO, ta có thể sử dụng định lý Thales và các quy tắc về tỉ lệ đồng dạng. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
b) Để chứng minh I là trung điểm của KH, ta có thể sử dụng các quy tắc về đường thẳng song song và đồng quy. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
c) Để chứng minh tứ giác AIEO là hình bình hành, ta có thể sử dụng các quy tắc về đường chéo và cạnh đối. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
d) Để chứng minh I, K, E thẳng hàng, ta có thể sử dụng các quy tắc về đường thẳng và góc vuông. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
Bạn tự vẽ hình nhé: nhớ **** cho mình với nhé...........
Gọi I và O thứ tự là giao điểm các đường chéo hình chữ nhật KMDN và ABCD.
Ta có: IN=ID=IK=IM ; OD=OC=OA=OB.
Do đó: góc N1=D1 ( tam giác NID cân do IN=ID )
góc D1=C1 ( tam giác DOC cân do OD=OC)
Mà góc N1=D1 ( đồng vị do EN song2 BD. Nên AC song2 KD.
Tứ giác EODI có EO song2 DI và EI song2 OD nên là hình bình hành.
=> OE=DI mà ID=KI nên OE=KI.
Tứ giác KEOI có KI song2 OE và KI song2 OE nên là hình bình hành.
=> KE song2 OI (1)
Tam giác KDB có OI là đường trung bình nên KB song2 OI (2)
Từ (1) và (2):=> K,E,B thẳng hàng ( tiên đề Euclide )
qua điểm E thuộc đg chéo BD của tgiac ABCD, vẽ EF//AD( F thuộc AB), EG//DC( G thuộc BC). cm: FG //AC
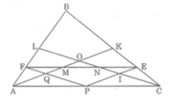
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL
Trong △ FPE ta có: PE//AK hay QM //PE
Suy ra: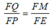 
(định lí ta-lét) (1)
Trong △ ALO ta có:PF //CL hay FQ //LO
Suy ra: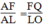
(định lí ta-lét) (2)
Trong △ ALC ta có: PF // CL
Suy ra: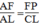 
(định lí ta-lét) (3)
Từ (2) và (3) suy ra: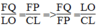 
Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên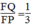 
(4)
Từ (1) và (4) suy ra: 
⇒ FM = 1/3 FE
Trong △ EPF ta có:PF // CL hay NI // PF
Suy ra: 
(định lí ta –lét) (5)
Trong △ CKO ta có: EI // OK
Suy ra: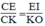 
(định lí ta –lét) (6)
Trong △ CKA ta có:PE // AK
Suy ra: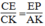 
(định lí ta –lét) (7)
Từ (6) và (7) suy ra: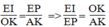 
Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên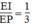 
(8)
Từ (5) và (8) suy ra: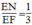 
⇒EN = 1/3 EF
Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF
Vậy EN = MN = NF
a) Xét tam giác ABC có: OE // BC (gt).
\(\Rightarrow\) \(\dfrac{AE}{AB}=\dfrac{AO}{AC}\left(Talet\right).\left(1\right)\)
Xét tam giác ACD có: OF // CD (gt).
\(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AO}{AC}\left(Talet\right).\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AE}{AB}.\)
Xét tam giác ABD có: \(\dfrac{AF}{AD}=\dfrac{AE}{AB}\left(cmt\right).\)
\(\Rightarrow\) EF // BD (định lý Talet đảo).
b: Xét tứ giác AEPF có
AE//PF
AF//PE
góc FAE=90 độ
=>AEPF là hcn
=>góc AEF=góc APF=góc ADB
=>FE//BD