Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

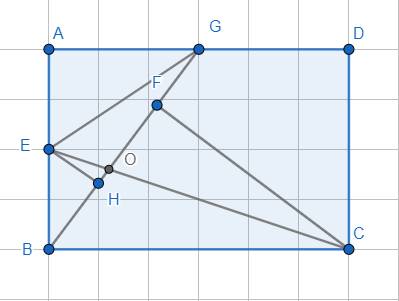
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)

S(ABCD)=600.S(NBC)=S(ABM)=150.S(ABC)=300..S(ANC)=S(AMC)=1/4S(ABCD).
Gọi MH và NI lần lượt là chiều cao của tam giác ANC và AMC.
MH=NI( dt ANC=AMC và chung đáy AC).
S(MFC)=S(NFC)(chung đáy FC và chiều cao MH=NI).
S(MFC)=S(MFB) (chung chiều cao hạ từ Fxuống BC và đáy MC=MB)
suy ra S(FMC)=1/3S(NBC)=1/3× 150
=50.S(AFM)
=S(ABC)-S(FMC)-S(ABM)
=300-50-150=100
S(BMN)=1/4S(ABN)
Gọi MK và AG lần lượt là chiều cao của tam giác BMN và ABN.
Suy ra: MK=1/4AG(▲ BMN=1/4▲ABN và chung đáy NB).
S(MEF)=1/4S(AEF)(chung đáy EF và chiều cao MK=1/4AG) hay S(AEF)=4/5×S(AMF)=4/5×100=80

S(ABCD)=600.S(NBC)=S(ABM)=150.S(ABC)=300..S(ANC)=S(AMC)=1/4S(ABCD). Gọi MH và NI lần lượt là chiều cao của tam giác ANC và AMC. MH=NI( dt ANC=AMC và chung đáy AC). S(MFC)=S(NFC)(chung đáy FC và chiều cao MH=NI). S(MFC)=S(MFB) (chung chiều cao hạ từ Fxuống BC và đáy MC=MB) suy ra S(FMC)=1/3S(NBC)=1/3× 150 =50.S(AFM) =S(ABC)-S(FMC)-S(ABM) =300-50-150=100 S(BMN)=1/4S(ABN) Gọi MK và AG lần lượt là chiều cao của tam giác BMN và ABN. Suy ra: MK=1/4AG( tam giác BMN=1/4tam giác ABN và chung đáy NB). S(MEF)=1/4S(AEF)(chung đáy EF và chiều cao MK=1/4AG) hay S(AEF)=4/5×S(AMF)=4/5×100=80

Ta có: * \(\frac{S_{\Delta ADE}}{S_{\Delta ADB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta ADB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta ADE}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta DCM}}{S_{\Delta DCB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta CDB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta DCM}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta EBM}}{S_{\Delta EBC}}=\frac{1}{2}\) mà \(\frac{S_{\Delta EBC}}{S_{\Delta ABC}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta EBM}}{S_{\Delta ABC}}=\frac{1}{4}\)
tuy nhiên \(\frac{S_{\Delta EBC}}{S_{ABCD}}=\frac{1}{4}\) suy ra \(\frac{S_{\Delta EBM}}{S_{ABCM}}=\frac{1}{8}\)
Ta lại có: \(\frac{S_{\Delta DEM}}{S_{ABCD}}=S_{ABCD}-\left(S_{\Delta ADE}+S_{\Delta EBM}+S_{\Delta DCM}\right)=1-\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{8}\right)=\frac{3}{8}\)
\(\Rightarrow\) \(S_{ABCD}=S_{\Delta DEM}\div\frac{3}{8}=6\times\frac{8}{3}=16\left(cm^2\right)\)