Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D P M
a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).
B A K H C E I D
Ta có \(\widehat{AHC}=\widehat{AEC}=90^0\) nên 4 điểm A, H, C, E cùng thuộc đường tròn đường kính AC.
Gọi I là giao điểm của AC và BD
Ta có \(\widehat{HIE}=2\widehat{HAE}=2\left(180^0-\widehat{BCD}\right)\)
Các tứ giác AKED, AKHB nội tiếp nên \(\widehat{EKD}=\widehat{EAD}\) và \(\widehat{BKH}=\widehat{BAH}\)
Do đó \(\widehat{HKE}=180^0-\widehat{AKD}-\overrightarrow{BKH}=180^0-\overrightarrow{EAD}-\overrightarrow{BAH}=2\overrightarrow{HAE}=2\left(180^0-\overrightarrow{BCD}\right)=\overrightarrow{HIE}\)
Vậy tứ giác HKIE nội tiếp. Do đó I thuộc đường tròn (C) ngoại tiếp tam giác HKE
- Gọi \(C\left(c;c-3\right)\in d\left(c>0\right)\Rightarrow I\left(\frac{c-2}{2};\frac{c-4}{2}\right)\)
Do I thuộc (C) nên có phương trình :
\(c^2-c-2=0\Leftrightarrow c=2\) V c=-1 (loại c=-1) Suy ra \(C\left(2;-1\right);I\left(0;-1\right)\)
- Điểm E, H nằm trên đường tròn đường kính AC và đường tròn (C) nên tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}x^2+y^2+x+4y+3=0\\x^2+\left(y+1\right)^2=4\end{cases}\) \(\Leftrightarrow\begin{cases}x=0;y=-3\\x=-\frac{8}{5};y=-\frac{11}{2}\end{cases}\)
- Vì H có hoành độ âm nên \(H\left(-\frac{8}{5};-\frac{11}{5}\right);E\left(0;-3\right)\) Suy ra \(AB:x-y+1=0;BC:x-3y-5=0\)
Tọa độ B thỏa mãn \(\begin{cases}x-y+1=0\\x-3y-5=0\end{cases}\) \(\Leftrightarrow B\left(-4;-3\right)\Rightarrow\overrightarrow{BA}=\left(2;2\right);\overrightarrow{BC}=\left(6;2\right)\Rightarrow\overrightarrow{BA}.\overrightarrow{BC}=16>0\)
Vì \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow D\left(4;1\right)\)
Vậy \(B\left(-4;-3\right);C\left(2;-1\right);D\left(4;1\right)\)
(a) phân giác trong y=-2 , phân giác ngoài x=2
(b) x=5
(c)x+15y+28=0
a)Xét tam giác BAD và BED(đều là ta giác vuông)
BD là cạnh chung
ABD=DBE(Vì BD là tia p/giác)
\(\Rightarrow\)tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)AB=BE(cặp cạnh tương ứng)
b)Vì tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)DA=DE(cặp cạnh tương ứng)
Xét tam giác ADF và EDCđều là ta giác vuông)
DA=DE(CMT)
ADF=EDC(đđ)
\(\Rightarrow\)tam giác ADF=tam giác EDC(cạnh góc vuông góc nhọn)
\(\Rightarrow\)DF=DC(cặp cạnh tương ứng)
Do đó tam giác DFC cân tại D(vì DF=DC)
c)Vì DA=DE(CMT)\(\Rightarrow\)tam giác DAE can tại D
Mà ADE=FDC(đđ)
Mà hai tam giác DAE và CDF cân
Do đó:DAE=DEA=DFC=DCF
\(\Rightarrow\)AE//FC vì DFC=DAE
Chọn B.
Xét đáp án B
Đặt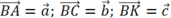
và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên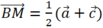
,
Do đó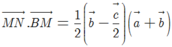
Vì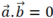
và 
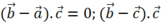nên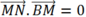 
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.