Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

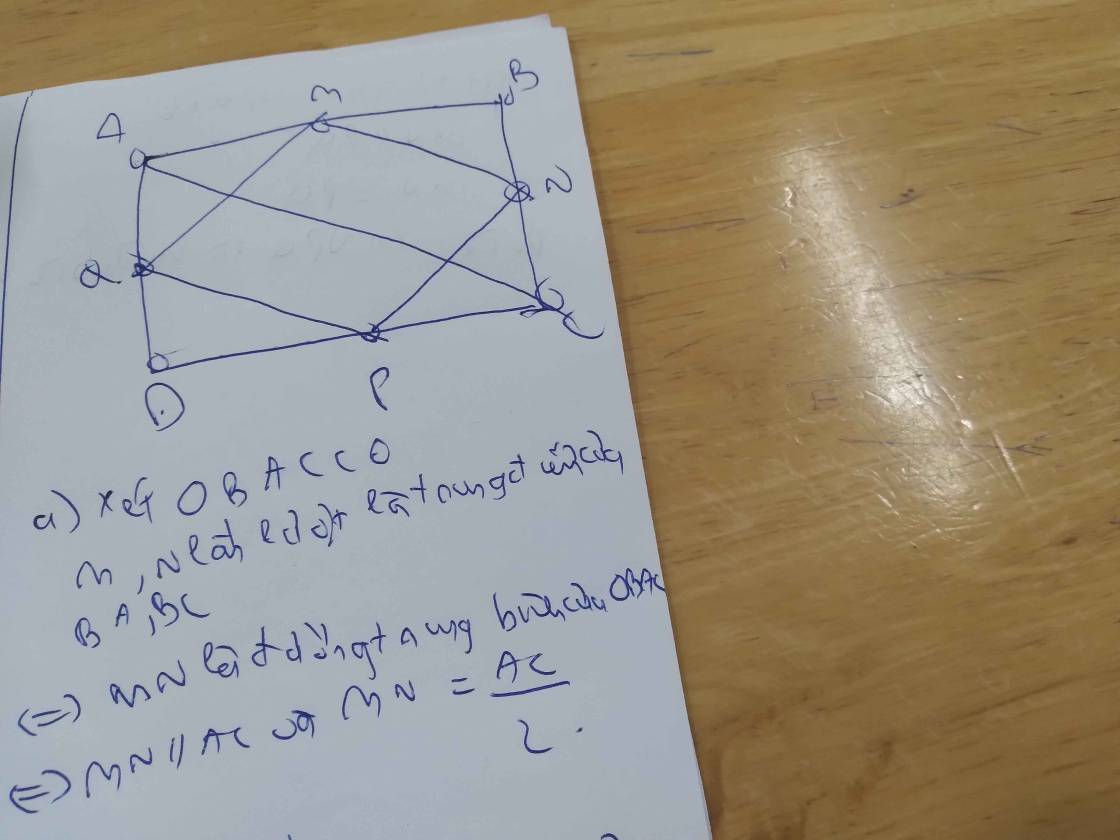
A B D C M N P Q Xét △ADC có:
AQ=QD và DP=PC
=>QP là đường trung bình=>QP//AC và QP=1/2 AC
Xét △ABC có:
AM=MB và BN=NC
=>MN là đường trung bình=>MN//AC và MN=1/2 AC
=>MN//QP và MN=QP
=>MNPQ là hbh
Xét △ABD có :
AQ=QD và MA=MB
=>QM là đường trung bình
=>QM=1/2 BD
Mà AC=BD (do ABCD là hcn)
=>QM=1/2 AC
=>QM=QP
=>MNPQ là h.thoi

Xét ΔADB có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP(3)
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2
mà MQ=BD/2
mà AC=BD
nên MN=MQ(4)
Từ (3) và (4) suy ra MNPQ là hình thoi

http://lazi.vn/edu/exercise/cho-tu-giac-abcd-goi-m-n-p-q-lan-luot-la-trung-diem-cua-cac-canh-ab-cd-ad-bc-chung-minh-vecto-mp-qn-mq-pn . Bạn vào link này nhé

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD


M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, AD
⇒ AM = MB; BN = NC; CP = DP; AQ = DQ
+ Xét Δ ABD có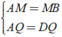
⇒ MQ là đường trung bình của Δ ABD.
⇒ QM = 1/2BD = 1/2AC ( 1 )
+ Xét Δ ABC có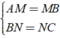
⇒ MN là đường trung bình của Δ ABC.
⇒ MN = 1/2BD = 1/2AC ( 2 )
+ Xét Δ BCD có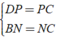
⇒ NP là đường trung bình của Δ BCD.
⇒ NP = 1/2BD = 1/2AC ( 3 )
+ Xét Δ ADC có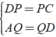
⇒ QP là đường trung bình của Δ ADC.
⇒ QP = 1/2BD = 1/2AC ( 4 )
Từ ( 1 ),( 2 ),( 3 ),( 4 ) ⇒ MN = NP = PQ = QM.
⇒ MNPQ là hình thoi.