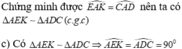Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

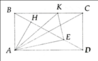
*Hình vẽ tay hơi xấu thông cảm
a, Ta có: \(\frac{DE}{DH}=\frac{CK}{BC}\Rightarrow\frac{DE}{CK}=\frac{DH}{BC}\left(1\right)\)
Gọi giao điểm của AC và BD là O.
=> OA = OB = OC = OD
=> ∆OBC cân tại O
=> ^OCB = ^OBC hay ^ACB = ^OBC
Xét ∆AHD và ∆ABC có:
^AHD = ^ABC
^ADH = ^ACB ( = ^OBC)
=> ∆AHD ~ ∆ABC (g-g)
=> \(\frac{AD}{AC}=\frac{DH}{BC}\left(2\right)\)
Từ (1) và (2) => \(\frac{AD}{AC}=\frac{DE}{DH}\)
Xét ∆ADE và ∆ACK có:
\(\frac{AD}{AC}=\frac{DE}{DH}\)(cmt)
^ADE = ^ACK ( vì ^ADH = ^ACB)
=> ∆ADE ~ ∆ACK (c-g-c)
b, Theo câu a, ∆ADE ~ ∆ACK
=>\(\hept{\begin{cases}\widehat{DAE}=\widehat{CAK}\Rightarrow\widehat{DAE}+\widehat{EAC}=\widehat{CAK}+\widehat{EAC}\Rightarrow\widehat{DAC}=\widehat{EAK}\\\frac{AE}{AK}=\frac{AD}{AC}\Rightarrow\frac{AE}{AD}=\frac{AK}{AC}\end{cases}}\)
=> ∆AEK ~ ∆ADC (c-g-c)

a) Xét ΔACB vuông tại B và ΔDBC vuông tại C có
AC=DB(hai đường chéo của hình chữ nhật ABCD)
BC chung
Do đó: ΔACB=ΔDBC(cạnh huyền-cạnh góc vuông)
⇒ΔACB∼ΔDBC(hai tam giác bằng nhau là hai tam giác đồng dạng)(1)
Xét ΔDBC vuông tại C và ΔADH vuông tại H có
\(\widehat{DBC}=\widehat{ADH}\)(hai góc so le trong, AD//BC)
Do đó: ΔDBC∼ΔADH(góc nhọn)(2)
Từ (1) và (2) suy ra ΔACB∼ΔADH
⇒\(\frac{BC}{DH}=\frac{AC}{AD}\)
⇒\(\frac{DH}{BC}=\frac{AD}{AC}\)(3)
Ta có: \(\frac{DE}{DH}=\frac{CK}{CB}\)
⇒\(\frac{DE}{CK}=\frac{DH}{BC}\)(4)
Từ (3) và (4) suy ra \(\frac{AD}{AC}=\frac{DE}{CK}\)
Xét ΔADB vuông tại A và ΔBCA vuông tại B có
BD=AC(hai đường chéo của hình chữ nhật ABCD)
AD=BC(hai cạnh đối của hình chữ nhật ABCD)
Do đó: ΔADB=ΔBCA(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{ADB}=\widehat{BCA}\)(hai góc tương ứng)
hay \(\widehat{ADE}=\widehat{ACK}\)
Xét ΔADE và ΔACK có
\(\frac{AD}{AC}=\frac{DE}{CK}\)(cmt)
\(\widehat{ADE}=\widehat{ACK}\)(cmt)
Do đó: ΔADE∼ΔACK(c-g-c)

Lời giải:
a) Xét tam giác $ADH$ và $ACB$ có:
$\widehat{ADH}=\widehat{ACB}$ (do tính chất hcn)
$\widehat{AHD}=\widehat{ABC}=90^0$
$\Rightarrow \triangle ADH\sim \triangle ACB$ (g.g)
$\Rightarrow \frac{AD}{AC}=\frac{DH}{CB}=\frac{DE}{CK}$
$\Rightarrow \triangle ADE\sim \triangle ACK$ (c.g.c)
b)
Từ tam giác đồng dạng phần a suy ra:
- $\widehat{DAE}=\widehat{CAK}$ (1)
$\Rightarrow \widehat{DAE}+\widehat{EAC}=\widehat{CAK}+\widehat{EAC}$
Hay $\widehat{DAC}=\widehat{EAK}$
- $\frac{AE}{AD}=\frac{AK}{AC}$ (2)
Từ $(1);(2)\Rightarrow \triangle AEK\sim \triangle ADC$ (c.g.c)
c)
$\Rightarrow \widehat{AEK}=\widehat{ADC}=90^0$ (đpcm)