Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
\(\left|\overrightarrow{BC}+\overrightarrow{BA}\right|=\left|\overrightarrow{AC}\right|=AC=a\sqrt{2}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)

a: \(\left|\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\left|\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\dfrac{\overrightarrow{AD}+\overrightarrow{AC}}{2}\right|\)
\(=\left|\dfrac{3\cdot\overrightarrow{AC}}{2}\right|=\dfrac{3}{2}AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}=7.5\)

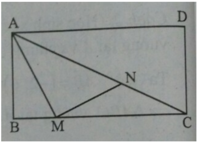
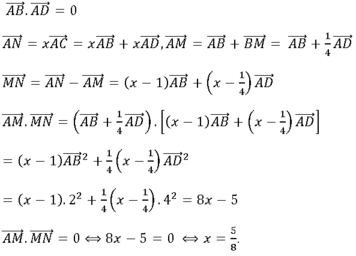
Chọn A.
Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình