Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

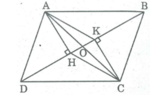
Ta có:
△ ABC = △ ADC (c.c.c) ⇒ S A B C = S A D C (1)
△ AHC = △ AKC (c.c.c) ⇒ S A H C = S A K C (2)
Từ (l) và (2) ⇒ S A B C + S A H C = S A D C + S A K C
Hay S A B C H = S A D C K

Bài giải:
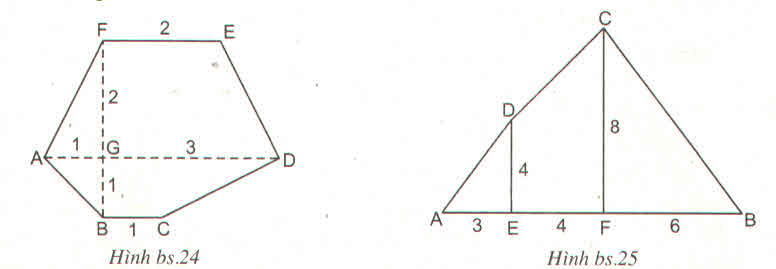
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

có tam giác ABD=BCD (c.c.c) suy ra CK=AH a b c d h k
xét tứ giác AKCH có ck=ah cmt hkc=ahk=90 độ ( so le trong ) -> ah//kc -> AKCH là hình bình hành (dhnb)-> CH=AK
xét tam giác ADK và BCH có BC=AD CH=AK cmt có góc ADH= góc CBK so le trong -> ADK=BCH (c.g.c)
xét tam giác ABH VÀ CKH = nhau (c.g.c) ( chứng minh tượng tự ) -
Ta có đa giác ABCH = AHB+CHD và ADCK=AKD+CKD MÀ AHB=Ckd cmt . ADK = BCH cmt -> tứ giác ABCH=ADCK-> diện tích=nhau