Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d\left(I;AB\right)=\frac{\left|\frac{1}{2}+2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\frac{\sqrt{5}}{2}\Rightarrow AD=2d\left(I;AB\right)=\sqrt{5}\)và \(AB=2AD=2\sqrt{5}\)
Do đó \(IA=IB=IC=ID=\frac{1}{2}AC=\frac{5}{2}\)
Gọi \(\omega\) là đường tròn tâm I, bán kính \(R=IA\) thế thì \(\omega\) có phương trình \(\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\)
Do vậy tọa độ của A, B là nghiệm của hệ :
\(\begin{cases}\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\\x-2y+2=0\end{cases}\)
Giải hệ thu được \(A\left(-2;0\right);B\left(2;2\right)\) (do A có hoành độ âm), từ đó , do I là trung điểm của AC và BD suy ra \(C\left(3;0\right);D\left(-1;-2\right)\)

Từ giả thiết suy ra điểm A không nằm trên 2 cạnh có phương trình đã cho. Bởi vậy, đó là phương trình của 2 đường thẳng chứa cạnh BC, CD, chẳng hạn \(BC:2x-3y+5\)
\(CD:3x+2y-7=0\)
Khi đó, đường thẳng chứa cạnh AB đi qua \(A\left(2;-3\right)\) và song song với đường thẳng CD, nên có phương trình :
\(3\left(x-2\right)+2\left(y+3\right)=0\)
hay : \(3x+2y=0\) ẳng chứa cạnh AD là :
\(2x-3y-11=0\)

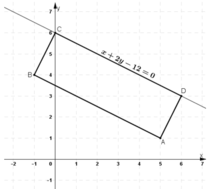
CD: x + 2y – 12 = 0 ⇒ CD nhận 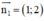 là một vtpt
là một vtpt
⇒ CD nhận 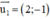 là một vtcp.
là một vtcp.
+ ABCD là hcn ⇒ AD ⊥ CD ⇒ AD nhận 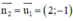 là một vtpt
là một vtpt
A(5 ; 1) ∈ AD
⇒ Phương trình đường thẳng AD: 2( x- 5) – 1(y – 1) = 0 hay 2x – y – 9 = 0.
+ ABCD là hcn ⇒ AB // CD ⇒ AB nhận 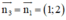 là một vtpt
là một vtpt
A(5;1) ∈ AB
⇒ Phương trình đường thẳng AB: 1( x- 5) + 2(y -1) = 0 hay x + 2y – 7 = 0
+ ABCD là hcn ⇒ BC ⊥ CD ⇒ BC nhận 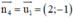 là một vtpt
là một vtpt
C(0, 6) ∈ CD
⇒ Phương trình đường thẳng BC: 2(x- 0)- 1(y – 6) =0 hay 2x – y + 6 = 0.

\(d\left(A\left(P\right)\right)=\frac{\left|2\left(-2\right)-2.1+1.5-1\right|}{\sqrt{2^2+\left(-2\right)^2+1^2}}=\frac{2}{3}\)
(P) có vectơ pháp tuyến là \(\overrightarrow{n_p}=\left(2;-2;1\right);\)
d có vectơ pháp tuyến là \(\overrightarrow{u_d}=\left(2;3;1\right);\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(-5;0;10\right)\)
Theo giả thiết suy ra (Q) nhận \(\overrightarrow{n}=-\frac{1}{5}\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(1;0;-2\right)\) làm vectơ pháp tuyến
Suy ra \(\left(Q\right):x-2z+12=0\)





Ta có: ABCD là hình chữ nhật nên AB // CD.
Khi đó AB có phương trình: x + 2y + m = 0
Mà A(5; 1) ∈ AB nên m = -7.
Vậy AB có phương trình: x + 2y – 7 = 0
Mặt khác AD ⊥ AB nên AD có phương trình là: 2x – y + n = 0
Mà A ∈ AD nên n = -9.
Vậy AD có phương trình: 2x – y – 9 = 0.
Vì BC // AD nên BC có phương trình: 2x – y + p = 0.
Mà C ∈ BC nên p = 6
Vậy CB có phương trình 2x – y + 6 = 0.