K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

S
13 tháng 1
a) xét từ giác ADMN có:
\(\widehat{MAD}=90^o\) (ABCD là hình chữ nhật)
\(\widehat{ADN}=90^o\) (ABCD là hình chữ nhật)
\(\widehat{DNM}=90^o\) (giả thiết)
⇒ từ giác ADMN là hình chữ nhật
b) xét từ giác ADBK có:
MA = MB (M là trung điểm AB)
MD = MK (M là trung điểm của DK)
⇒ từ giác ADBK là hình bình hành
Ta có : BD = AK (vì tứ giác ADBK là hình bình hành) (1)
Lại có: AC = BD (vì ABCD là hình chữ nhật) (2)
Từ (1) và (2) ⇒ AK = AC
⇒ ΔACK là Δ cân tại A

CM
16 tháng 8 2019
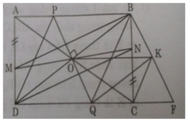
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.