

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án là C.
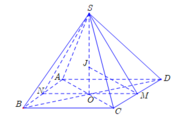
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO
V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .
Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a
Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.
Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .
Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6

Đáp án D
Gọi O là tâm của hình vuông A B C D ⇒ S O ⊥ A B C D
vÌ S O ⊥ A B C D suy ra S A ; A B C D ^ = S A ; O A = S A O ^ ^ = 60 0
Tam giác S A O vuông tại O, Có tan S A O ^ = S O O A ⇒ S O = tan 60 0 . a 2 2 = a 6 2
Vậy thể tích khối chóp là V = 1 3 . S O . S A B C D = 1 3 . a 6 2 . a 2 = a 3 6 6

Đáp án C.
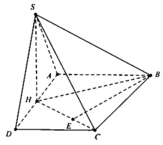
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....

Đáp án C
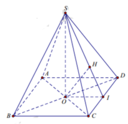
Vì A B / / C D nên d A B ; S C = d A B ; S C D
= d A ; S C D = 2 d O ; S C D = 2 O H , trong đó I là trung điểm của CD và H là hình chiếu vuông góc của O xuống SI.
Ta có: O I = a 2 ; S I = a 2 − a 2 2 = a 3 2 ; S O = a 3 2 2 − a 2 2 = a 2 2
1 O H 2 = 1 O S 2 + 1 O I 2 = 1 a 2 2 2 + 1 a 2 2 = 6 a 2 ⇒ O H = a 6
⇒ d A B ; S C = 2. a 6 = a 6 3

Đáp án A
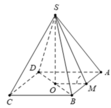
Xét hình chóp tứ giác đều S.ABCD có các cạnh bằng a.
Gọi O là tâm hình vuông ABCD, M là trung điểm của AB.
Khi đó S O ⊥ A B O M ⊥ A B ⇒ A B ⊥ S M O ⇒ S A B ; A B C D ^ = S M O ^
Tam giác SMO vuông tại O, có c o s S M O ^ = O M S M = a 2 : a 3 2 = 3 3
Vậy c o s S A B ; A B C D ^ = 3 3