Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
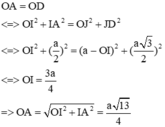
Ta có:

Đáp án C.
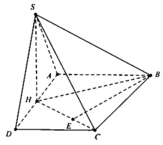
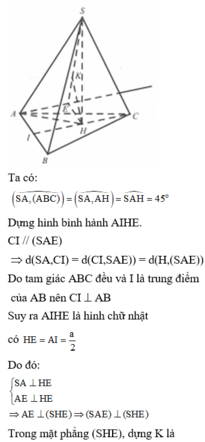
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .




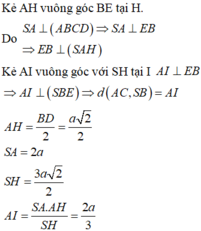



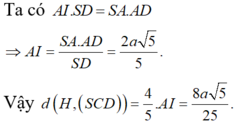

Đáp án C.
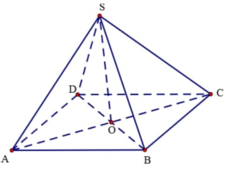
Gọi O chân đường cao hạ từ S xuống mặt đáy ⇒ A C ∩ B D = O .
Dựng O H ⊥ S N (H thuộc SN). Gọi M, N lần lượt là trung điểm của AD và BC. Trong (SMN), kẻ M I // O H (I thuộc SN).
Em có: AD//BC⇒d S B , A D = d A D , S B C = d M , S B C .
Em lại có: S M N ⊥ S B C ⇒ OH ⊥ S B C
Do O H // M I nên MI⊥SBC⇒d M , S B C = M I = 2 O H .
Tam giác SON vuông tại O, đường cao OH nên ta có
1 O H 2 = 1 S O 2 + 1 O N 2 ⇒ O H = a h 4 h 2 + a 2 ⇒ M I = 2 a h 4 h 2 + a 2