Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng a 3 2 . Tính số đo của góc giữa mặt bê...

Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng a...

BM

Bùi Mạnh Dũng

9 tháng 12 2016

cho hình chóp SABCD là hình thoi có cạnh bằng a\(\sqrt{3}\) ,góc BAD bằng \(120^0\) và cạnh bên SA vuông góc với mặt phẳng đáy.Biết rằng số đo của góc giữa hai mặt phẳng(SBC) và đáy bằng \(60^0\).khoảng cách giữ hai đường thẳng BD và SC bằng

#Toán lớp 11

0

BM

Bùi Mạnh Dũng

9 tháng 12 2016

cho hình chóp SABCD là hình thoi có cạnh bằng a\(\sqrt{3}\) ,góc BAD bằng \(120^0\) và cạnh bên SA vuông góc với mặt phẳng đáy.Biết rằng số đo của góc giữa hai mặt phẳng(SBC) và đáy bằng \(60^0\).khoảng cách giữ hai đường thẳng BD và SC bằng

#Toán lớp 11

0

SG

Sách Giáo Khoa

23 tháng 5 2017

Cho hình lăng trụ tam giác ABC.A'B'C' có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc \(60^0\) và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'

a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ

b) Chứng minh rằng mặt bên BCC'B' là một hình vuông

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

Đúng(0)

MC

Meo Con Nguyen

23 tháng 5 2016

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA=a\(\sqrt{2}\)

a) CMR các mặt bên của hình chóp là những tam giác vuông.

b) CMR (SAC) vuông góc với (SBD)

c)Tính góc giữa SC và mp (SAB)

d)Tính góc giữa hai mp(SBD) và (ABCD)

e)Tính khoảng cách giữa điểm A và mp (SCD).

#Toán lớp 11

4

HT

Hồng Trinh

23 tháng 5 2016

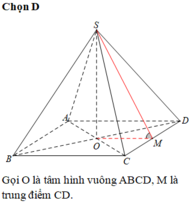
a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)

tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)

ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)

Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)

Đúng(0)

HT

Hồng Trinh

23 tháng 5 2016

b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)

Đúng(0)

SG

Sách Giáo Khoa

31 tháng 3 2017

Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a có góc \(\widehat{BAD}=60^0\) và \(SA=SB=SD=\dfrac{a\sqrt{3}}{2}\) : a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD) c) Chứng minh SB vuông góc với BC d) Gọi \(\varphi\) là góc giữa hai mặt phẳng (SBD) và (ABCD)....

Đọc tiếp

#Toán lớp 11

2

QD

Quang Duy

31 tháng 3 2017

Giải bài 7 trang 122 sgk Hình học 11 | Để học tốt Toán 11

Đúng(0)

QD

Quang Duy

31 tháng 3 2017

Giải bài 7 trang 122 sgk Hình học 11 | Để học tốt Toán 11

Đúng(0)

SG

Sách Giáo Khoa

31 tháng 3 2017

Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng \(60^0\), cạnh \(SC=\dfrac{a\sqrt{6}}{2}\) và SC vuông góc với mặt phẳng (ABCD) a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK c) Chứng minh \(\widehat{BKD}=90^0\) và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng...

Đọc tiếp

#Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 11 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Đúng(1)

SG

Sách Giáo Khoa

23 tháng 5 2017

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và \(SA\perp\left(ABCD\right)\)

a) Chứng minh \(BD\perp SC\)

b) Chứng minh \(\left(SAB\right)\perp\left(SBC\right)\)

c) Cho \(SA=\dfrac{a\sqrt{6}}{3}\). Tính góc giữa SC và mặt phẳng (ABCD)

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

Đúng(0)

SG

Sách Giáo Khoa

31 tháng 3 2017

Hình chóp A.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA bằng a và vuông góc với mặt phẳng (ABCD)

a) Chứng minh rằng các mặt bên kia của hình chóp là những tam giác vuông

b) Mặt phẳng \(\left(\alpha\right)\) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, SC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB

#Toán lớp 11

1