Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(SM=MA=SA-SM\Rightarrow SM=\dfrac{1}{2}SA\)
Do IM song song SO, áp dụng định lý Talet trong tam giác SAO:
\(\dfrac{IO}{OA}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Do NK song song SO, áp dụng định lý Talet cho tam giác SCO:
\(\dfrac{OK}{OC}=\dfrac{SN}{SC}=\dfrac{1}{3}\)
Mà ABCD là hình bình hành nên \(OA=OC\)
\(\Rightarrow\dfrac{OI}{OK}=\dfrac{3}{2}\)
Tham khảo:
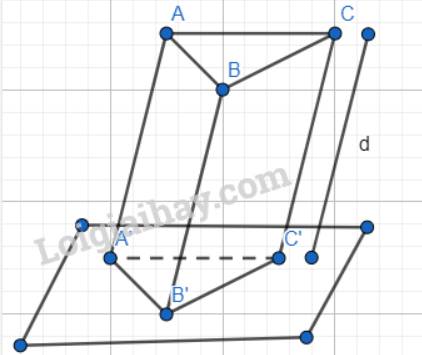
Nếu tam giác A′B′C′ là hình chiếu của tam giác ABC theo phương d thì tam giác ABC là hình chiếu của tam giác A′B′C′ vì tam giác ABC là tập hợp tất cả các hình chiếu của các điểm thuộc A'B'C' qua phép chiếu song song theo phương d.
Do AB||CD, áp dụng Talet:
\(\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{1}{2}\Rightarrow\dfrac{OB}{OD}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{OB}{OD}=\dfrac{MB}{MS}\Rightarrow OM||SD\)
\(\Rightarrow OM||\left(SCD\right)\)
Trong mp (ABCD), qua O kẻ đường thẳng song song AB cắt AD và BC lần lượt tại E và F
Trong mp (SAB), qua M kẻ đường thẳng song song AB cắt SA tại P
\(\Rightarrow\) Hình thang PMFE là thiết diện của mặt phẳng và chóp
a: Xét hình thang ABCD có
M,N lần lượt là trung điểm của AB,CD
nên MN là đường trung bình
=>MN//AD//BC
=>MN//(SAD) và MN//(SBC)
b: Gọi giao của MN với BD là O
=>O thuộc (SBD) giao (MNP)
MP//SB
=>\(\left(SBD\right)\cap\left(MNP\right)=xy\left(O\in xy\right);\)xy//MP//SB
Gọi M là trung điểm của SA
Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
=>MN//BC
=>M là hình chiếu song song của N theo phương BC lên mp(SAB)
Gọi N là trung điểm của SD
Xét ΔSCD có
M,N lần lượt là trung điểm của SC,SD
=>MN là đường trung bình của ΔSCD
=>MN//CD
=>MN//AB
=>N là hình chiếu song song của M theo phương AB lên mp(SAD)
