Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
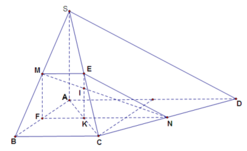
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và 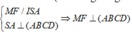
hay tứ giác MENF là hình thang vuông tại M, F
![]()
![]()
Ta có: 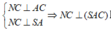 hay E là hình chiếu vuông góc của N lên (SAC)
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì ![]()
![]()
![]()
![]()

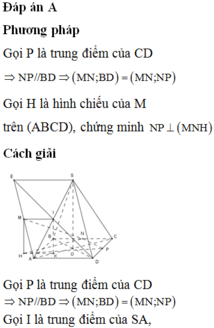
Gọi P là trung điểm của SA. Ta có MNCP là hình bình hành nên MN song song với mặt phẳng (SAC). Mặt khác, BD vuông góc với mặt phẳng (SAC) nên BD vuông góc với MN.
Vì MN song song với mặt phẳng (SAC) nên
\(d\left(MN,AC\right)=d\left(N,SAC\right)\)
\(=\frac{1}{2}d\left(B;\left(SAC\right)\right)=\frac{1}{4}BD=\frac{a\sqrt{2}}{4}\)
Vậy \(d\left(MN;AC\right)=\frac{a\sqrt{2}}{4}\)

Chọn A.
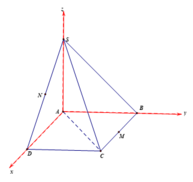
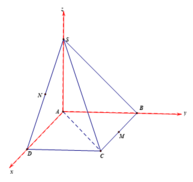
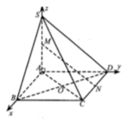
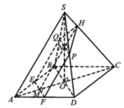
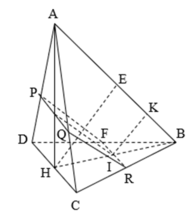
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:
A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)
M là trung điểm của BC ⇒ M a 2 ; a ; 0
N là trung điểm của SD ⇒ N a 2 ; 0 ; a 2 ⇒ M N → 0 ; - a ; a 2
Do ABCD là hình vuông nên AC ⊥ BD
S A ⊥ ( A B C D ) B D ⊂ ( A B C D ) ⇒ S A ⊥ B D
Ta có:
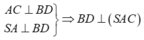
![]()
là một pháp tuyến của (SAC)
Khi đó ta có:
sin α = cos ( M N → , B D → ) = M N → . B D → M N → . B D →
= a 2 a 5 2 . a 2 = 10 5
1 sin 2 α = 1 + c o t 2 α ⇔ 25 10 = 1 + c o t 2 α ⇔ c o t 2 α = 3 2 ⇒ c o t α = 3 2 ( d o 0 < α < 90 0 )
Lại có:
tan α . c o t α = 1 ⇒ tan α = 2 3 = 6 3

Chọn A.
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:
A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)
M là trung điểm của BC ⇒ M a 2 ; a ; 0
N là trung điểm của SD ⇒ N a 2 ; 0 ; a 2 ⇒ M N → 0 ; - a ; a 2
Do ABCD là hình vuông nên AC ⊥ BD
S A ⊥ ( A B C D ) B D ⊂ ( A B C D ) ⇒ S A ⊥ B D
Ta có:
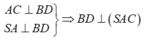
![]()
là một pháp tuyến của (SAC)
Khi đó ta có:
sin α = cos ( M N → , B D → ) = M N → . B D → M N → . B D →
= a 2 a 5 2 . a 2 = 10 5
1 sin 2 α = 1 + c o t 2 α ⇔ 25 10 = 1 + c o t 2 α ⇔ c o t 2 α = 3 2 ⇒ c o t α = 3 2 ( d o 0 < α < 90 0 )
Lại có:
tan α . c o t α = 1 ⇒ tan α = 2 3 = 6 3
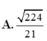
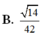
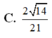
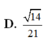
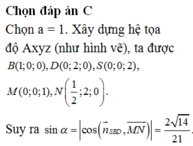
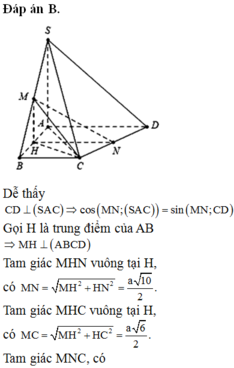
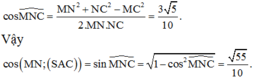
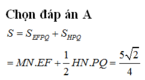
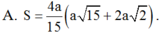

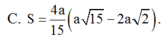
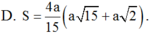


Đáp án B
Thật vậy, giả sử M N / / B C Ta sẽ chứng minh thiết diện là hình thang.
Khi đó, thiết diện là tứ giác J M J N
Do đó, tứ giác J M J N là hình thang (đpcm)