Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Kẻ \(CE//BD\Rightarrow BD//\left(SCE\right)\Rightarrow d\left(SC,BD\right)=d\left(BD,\left(SCE\right)\right)=d\left(B,\left(SCE\right)\right)\)
\(AB\cap\left(SCE\right)=\left\{E\right\}\Rightarrow\dfrac{d\left(B,\left(SCE\right)\right)}{d\left(A,\left(SCE\right)\right)}=\dfrac{EB}{EA}=\dfrac{1}{2}\)
\(\widehat{CAE}=\dfrac{1}{2}\widehat{DAB};\widehat{AEC}=\widehat{BDC}=\dfrac{1}{2}\widehat{ADC};\widehat{DAB}+\widehat{ADC}=180^0\Rightarrow\widehat{CAE}+\widehat{AEC}=90^0\Rightarrow\widehat{ACE}=90^0\)
\(\Rightarrow AC\perp EC\)
\(\left\{{}\begin{matrix}SA\perp CE\\AC\perp CE\end{matrix}\right.\Rightarrow CE\perp\left(SAC\right)\Rightarrow\left(SCE\right)\perp\left(SAC\right)\)
Kẻ \(AH\perp SC\Rightarrow AH\perp\left(SCE\right)\Rightarrow d\left(A,\left(SCE\right)\right)=AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=..\)
\(\Rightarrow d\left(SC,BD\right)=d\left(B,\left(SCE\right)\right)=\dfrac{AH}{2}=...\)
b/ \(AD//BC\Rightarrow AD//\left(SBC\right)\Rightarrow d\left(SC,AD\right)=d\left(AD,\left(SBC\right)\right)=d\left(A,\left(SBC\right)\right)\)
Kẻ \(AK\perp BC\Rightarrow\left\{{}\begin{matrix}SA\perp BC\\AK\perp BC\end{matrix}\right.\Rightarrow\left(SBC\right)\perp\left(SAK\right)\)
Kẻ \(AM\perp SK\Rightarrow AM\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AM=\dfrac{SA.AK}{\sqrt{SA^2+AK^2}}=...=d\left(SC,AD\right)\)

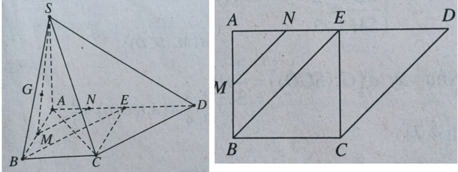
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).

a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ

Bạn chỉ nên đăng 1 bài 1 lần thôi, tránh làm loãng box toán!

Lời giải:
Vì $SA\perp (ABCD)$ nên
$60^0= \angle (SC, (ABCD))=\angle (SC, AC)=\widehat{SCA}$
Ta có:
$AC=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
$\frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{15}a$
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}$
$=\frac{1}{3}.\sqrt{15}a.a.2a=\frac{2\sqrt{15}}{3}a^3$

Đề bài sai. (SAD) và (SAC) cùng vuông góc với đáy, thế thì ta sẽ có là hình thoi ACBD, vô lý


