Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Cho hình chóp S.ABCD
a: Trong mp(ABCD), gọi K là giao điểm của AD và BC
\(K\in AD\subset\left(SAD\right)\)
\(K\in BC\subset\left(SBC\right)\)
Do đó: \(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SK\)
b: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD

a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)

Gọi E là giao điểm của AC và BD \(\Rightarrow\left\{{}\begin{matrix}E\in\left(SAC\right)\\E\in\left(SBD\right)\end{matrix}\right.\)
\(\Rightarrow SE=\left(SAC\right)\cap\left(SBD\right)\)
Kéo dài AD và BC cắt nhau tại F
\(\Rightarrow SF=\left(SAD\right)\cap\left(SBC\right)\)
b.
Chắc là trung điểm của SC và SD?
M và trung điểm SC, N là trung điểm SD
\(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN//CD\) , mà \(CD//AB\Rightarrow MN//AB\Rightarrow MN//\left(SAB\right)\)

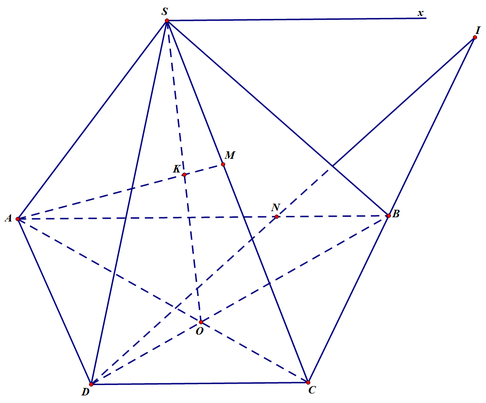
a, Gọi O là giao điểm của AC và BD
⇒ SO = (SAC) \(\cap\) (SBD)
b, (SAB) và (SCD) cùng đi qua điểm S và lần lượt chứa hai đường thẳng AB & CD, mà ta lại có AB // CD
⇒ (SAB) \(\cap\) (SCD) = Sx. trong đó Sx là đường thẳng đi qua S và song song với AB và CD
c, Trong (SAC) gọi K là giao điểm của SO và AM
⇒ AM \(\cap\) (SBD) = K
d, Trong (ABCD) gọi I = DN \(\cap\) BC
⇒ DN \(\cap\) (SBC) = I

Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)
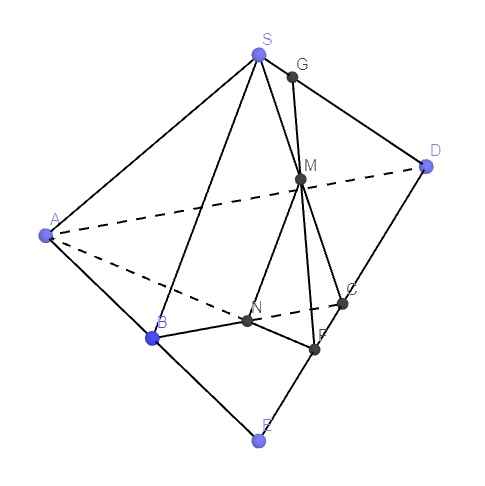
c: Điểm O ở đâu vậy bạn
Lúc nãy mik viết đề sai. Đề này mới đúng