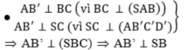Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do SA ⊥ (ABCD) ⇒ \(\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\\SA\perp BC\end{matrix}\right.\)
Mà BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC và BC ⊥ AH
Do BC ⊥ AH và AH ⊥ SC ⇒ AH ⊥ (SBC) ⇒ AH ⊥ KH ⇒ \(\widehat{AHK}=90^0\)
ΔSAB và ΔSAC vuông tại A
Mà AH và AK lần lượt là đường cao của ΔSAB và ΔSAC
⇒ \(\left\{{}\begin{matrix}SA^2=SK.SB\\SA^2=SH.SC\end{matrix}\right.\)
⇒ SK . SB = SH . SC
⇒ \(\dfrac{SK}{SH}=\dfrac{SC}{SB}\) ⇒ ΔSKH \(\sim\) ΔSCB ⇒ \(\widehat{SKH}=\widehat{SCB}=90^0\)
⇒ HK ⊥ SB
Mà AK⊥ SB
⇒ ((SAB),(SCB)) = (AK,AH) = \(\widehat{KAH}\) = 450 (đây là góc nhọn, vì \(\widehat{AHK}=90^0\))
⇒ ΔHAK vuông cân tại H ⇒ AK = \(\sqrt{2}AH\)
Ta có : \(\dfrac{S_{SAC}}{S_{SAB}}=\dfrac{\dfrac{1}{2}.AH.SC}{\dfrac{1}{2}AK.SB}=\dfrac{\dfrac{1}{2}.SA.AC}{\dfrac{1}{2}.SA.AB}\)
⇒ \(\dfrac{AH.SC}{AK.SB}=\dfrac{SA.AC}{SA.AB}\)
⇒ \(\dfrac{1}{\sqrt{2}}\) . \(\dfrac{SC}{SB}\) = \(\dfrac{AC}{AB}\). Mà AC = a và AB = 2a
⇒ \(\dfrac{1}{\sqrt{2}}\)\(\dfrac{SC}{SB}\) = \(\dfrac{1}{2}\) ⇒ \(\dfrac{SC^2}{SB^2}\) = \(\dfrac{1}{2}\) . Mà SB2 - SC2 = BC2 = 3a2
⇒ \(\left\{{}\begin{matrix}SC^2=3a^2\\SB^2=6a^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}SB=a\sqrt{6}\\SC=a\sqrt{3}\end{matrix}\right.\) ⇒ SA = a\(\sqrt{2}\)
Từ đó ta tính được SH = \(\dfrac{2a\sqrt{3}}{3}\) và SK = \(\dfrac{a\sqrt{6}}{3}\)
Gọi M là trung điểm của SB thì ta có CM // HK (cùng vuông góc với SB)
Khoảng cách từ HK đến AC bằng khoảng cách từ HK đến (AMC)
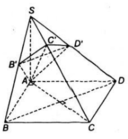
a/ Ta có: AB vuông góc với BC, SC vuông góc với BC (vì SC vuông góc với mặt đáy ABCD). Vậy AB // SC. Vậy AB vuông góc (SBC).
b/ Tương tự, ta có: AD vuông góc với CD, SC vuông góc với CD. Vậy AD // SC. Vậy AD vuông góc (SCD).
c/ Ta có: SA vuông góc với mặt đáy ABCD (vì S là đỉnh chóp), CI vuông góc với SB (vì đường thẳng CI là hình chiếu của đường thẳng SC lên mặt phẳng chứa SB và CI). Vậy SA // CI. Vậy SA vuông góc CI.
d/ Gọi M là trung điểm của IJ. Ta cần chứng minh SA vuông góc CM. Ta có: CM vuông góc với IJ (vì nằm trên đường trung trực của IJ). Ta cũng có: SA vuông góc CI (đã chứng minh ở câu c). Vậy ta cần chứng minh CI // JM. Từ đó suy ra (SAC) ⊥ (CIJ). Theo tính chất của hình học không gian, ta có CI vuông góc với mặt phẳng (SBC). Tương tự, JI vuông góc với mặt phẳng (SCD). Vậy CI // JI. Điều này suy ra từ tính chất của mặt phẳng và đoạn thẳng vuông góc với mặt phẳng. Suốt đoạn thẳng IJ, ta có thể lấy một điểm nào đó làm trung điểm, ví dụ M. Vậy CI // JM.
(ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)
a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ