Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

Chọn C
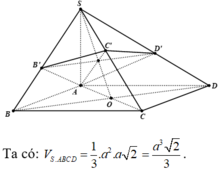
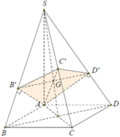
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
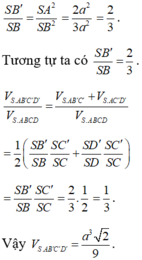


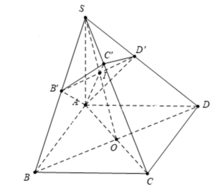
Do \(SA=SB=SC=SD\) và đáy là hình vuông nên \(SABCD\) là chóp đều
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Theo tính đối xứng của chóp đều \(\Rightarrow SB'=SD'\Rightarrow B'D'||BD\)
Gọi M là giao điểm SO và AC' \(\Rightarrow M\in B'D'\) (t/c giao tuyến 3 mp cắt nhau)
Áp dụng định lý Talet:
\(\dfrac{SM}{SO}=\dfrac{SD'}{SD}=\dfrac{SB'}{SB}=\dfrac{2}{3}\Rightarrow M\) là trọng tâm tam giác SAC
\(\Rightarrow C'\) là trung điểm SC \(\Rightarrow\dfrac{SC'}{SC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{V_{SAB'C'D'}}{V_{SABCD}}=\dfrac{2V_{SAB'C'}}{2V_{SABC}}=\dfrac{V_{SAB'C'}}{V_{SABC}}=\dfrac{SA}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=1.\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)

Đáp án D
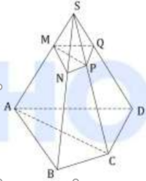

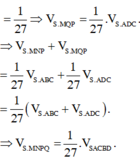
Chú ý: Em nhớ rằng, công thức tính tỉ số thể tích chỉ áp dụng cho khối chóp tam giác. Còn với khối chóp tứ giác, ngũ giác, lục giác,… em cần chia ra thành các khối chóp tam giác và áp dụng công thức.
Công thức giải nhanh:
Cắt khối chóp bởi mặt phẳng song song với đáy: Xét khối chóp S . A 1 A 2 . . . . . A n , mặt phẳng (P) song song với mặt đáy cắt cạnh S A 1 tại m thỏa mãn . Khi đó (P) chia khối chóp thành 2 khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V' và khối đa diện ban đầu có thể tích V thì V ' V = k 3
Nên ⇒ V S . M N P Q V S . A B C D = 1 3 2 = 1 27

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
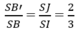
Do đó dễ thấy
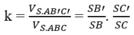
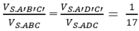
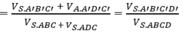
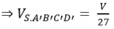
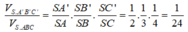
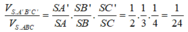

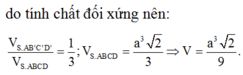

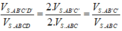
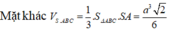
Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)